Lohéac J., Trélat E., Zuazua E. Minimal controllability time for the heat equation under unilateral state or control constraints . Mathematical Models and Methods in Applied Sciences, Volume 27, Issue 09, August 2017 DOI: 10.1142/S0218202517500270
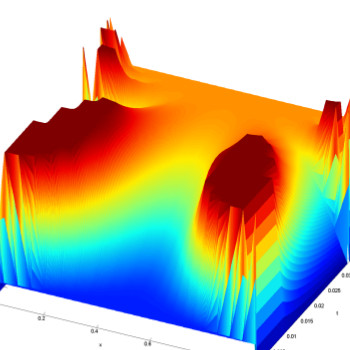
Abstract: The heat equation with homogeneous Dirichlet boundary conditions is well known to preserve non-negativity. Besides, due to infinite velocity of propagation, the heat equation is null controllable within arbitrary small time, with controls supported in any arbitrarily open subset of the domain (or its boundary) where heat diffuses. The following question then arises naturally: can the heat dynamics be controlled from a positive initial steady state to a positive final one, requiring that the state remains non-negative along the controlled time-dependent trajectory? We show that this state-constrained controllability property can be achieved if the control time is large enough, but that it fails to be true in general if the control time is too short, thus showing the existence of a positive minimal controllability time. In other words, in spite of infinite velocity of propagation, realizing controllability under the unilateral non-negativity state constraint requires a positive minimal time. We establish similar results for unilateral control constraints. We give some explicit bounds on the minimal controllability time, first in 1D by using the sinusoidal spectral expansion of solutions, and then in the multi-dimensional case. We illustrate our results with numerical simulations, and we discuss similar issues for other control problems with various boundary conditions.