Two recurring questions pertain to the origin, history, and present state of mathematics. The first relates to math’s incredible ability to describe natural, industrial, and technological processes, while the second concerns the unity and interconnectedness of all mathematical disciplines. Here I describe some of the gateways that link two particular mathematical branches: control theory and machine learning (ML). These areas, both of which have very high technological impacts, comprise neighboring valleys in the complex landscape of the mathematics universe.
Control theory certainly lies at the pedestal of ML. Aristotle anticipated control theory when he described the need for automated processes to free human beings from their heaviest tasks [3]. In the 1940s, mathematician and philosopher Norbert Wiener redefined the term “cybernetics”—which was previously coined by André-Marie Ampère—as “the science of communication and control in animals and machines,” which reflected the discipline’s definitive contribution to the industrial revolution.
Wiener’s definition involves two essential conceptual binomials. The first is control-communication: the need for sufficient and quality information about a system’s state to make the right decisions, reach a given objective, or avoid risky regimes. The second binomial is animal-machine. As Aristotle predicted, human beings rationally aim to build machines that perform tasks that would otherwise prevent them from dedicating time and energy to more significant activities. The close link between control and/or cybernetics and ML is thus built into Wiener’s own definition.
The interconnections between different mathematical disciplines are split by conceptual and technical mountain ranges and have often evolved in different communities. As such, they are frequently hard to observe. Building the connecting paths and identifying the hypothetical mountain passes requires an important level of abstraction. Let us take a step back and consider a wider perspective.
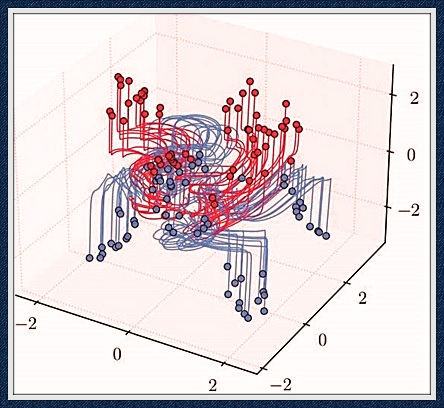
Figure 1. Simultaneous control of trajectories of a neural ordinary differential equation (NODE) for classification according to two different labels (blue/red), exhibiting the turnpike nature of trajectories. Figure courtesy of [5].
The notion of controllability helps us disclose one of the gateways between disciplines. Controllability involves driving a dynamical system from an initial configuration to a final one within a given time horizon via skillfully designed and viable controls. In the framework of linear finite N-dimensional systems
x′+Ax=Bu,
the answer is elementary and classical (it dates back to Rudolf Kalman’s work in the 1950s, at least) [6]. The system is controllable if and only if the matrix A that governs the system’s dynamics and the matrix B that describes the controls’ effects on the state’s different components verify the celebrated rank condition
rank[B,AB,…AN−1B]=N.
The control’s size naturally depends on the length of the time horizon; it must be enormous for very short time horizons and can have a smaller amplitude for longer ones.
In fact, as John von Neumann anticipated and Nobel Prize-winning economist Paul Samuelson further analyzed, the “turnpike” property manifests itself over long time horizons; controls tend to spend most of their time in the optimal steady-state configuration [5]. We apply this lesser-known principle systematically (and often unconsciously) in our daily lives. When travelling to work, for instance, we may rush to the station to take the train—our turnpike in this ride—on which we then wait to reach our final destination. Medical therapies for chronic diseases also utilize this principle; physicians may instruct patients to take one pill a day after breakfast, rather than follow a sharper but much more complicated dosage. This property even arises in the field of economics when national banks set interest rates in six-month horizons and only revisit the policies to adjust for newly emerging macroeconomic scenarios.
Are these ideas and methods at all relevant to ML?
(…)
The full article was originally published here.