1. El momento de las Matemáticas.
Las Matemáticas son a la vez una ciencia básica, el lenguaje en el que está escrito el universo, como decía Galileo Galilei, y también una disciplina que interacciona permanentemente con todos los demás ámbitos de nuestra sociedad.
En efecto, la sociedad actual reposa cada vez más en la comprensión que las Matemáticas aportan y que están en la base de la innovación en tecnología, ciencia, transporte, comunicaciones, etc. Por otra parte, las crecientes demandas de progreso exigen de un esfuerzo añadido en investigación matemática.
En este artículo presentamos un breve panorama de las matemáticas que se desarrollan en el campo del diseño óptimo, orientándonos al ámbito aeronáutico y haciendo especial énfasis en algunos de los problemas más relevantes aún por resolver, que tienen una motivación fuertemente tecnológica y a la vez un marcado acento matemático.
Las Matemáticas son una ciencia amplia, que abarca diferentes campos entre los que destaca la Matemática Aplicada, que tiene como uno de sus principales objetivos contribuir a la comprensión y al diseño de numerosos mecanismos y estructuras de gran importancia en nuestra vida diaria y en muy diversos ámbitos del I+D+i, haciéndolos más funcionales, más económicos, más respetuosos con el medio ambiente, más atractivos, etc. Este es el principal cometido de la disciplina del Diseño óptimo a la que dedicamos esta artículo. Sus aplicaciones son muy variadas: Biotecnología y Biomedicina (sistema cardiovascular, el diseño de bypasses y fármacos), Física Cuántica (control láser en Mecánica Cuántica, diseño molecular, nano-estructuras, opto-electrónica), estructuras y edificios inteligentes (en particular, que resistan los temblores sísmicos), Ingeniería Química (reactores y columnas de destilación), medioambiente (descontaminación, diques, reducción del ruido, la barrera del Támesis), sistemas de comunicaciones e irrigación, prospección y extracción de recursos naturales, aeronáutica, automoción, robótica,…
En el ámbito de la aeronáutica, en el que nos centramos en este artículo, uno de los principales objetivos de las Matemáticas es contribuir al diseño de aeronaves más seguras, eficaces y respetuosas con el medio ambiente.
Como veremos, a pesar de la complejidad de la empresa o, más bien, precisamente por eso, la Matemática Aplicada juega un importante papel.
Son ya muchos años de investigación matemática en este campo desde que los hermanos Wright, hace ahora algo más de un siglo, se convirtieran en los pioneros del aire. Pero es aún mucho lo que queda por hacer para ser capaces de realizar simulaciones numéricas lo bastante rápidas y eficaces que permitan desarrollar herramientas interactivas que sirvan a los diseñadores e ingenieros trabajar con un conocimiento fiable del rendimiento previsible de sus diseños en tiempo real. Las grandes empresas del sector y los más prestigiosos laboratorios científicos se afanan en este empeño, en el que las Matemáticas tienen mucho que aportar. A pesar de los importantes avances que se producen constantemente en la capacidad de cómputo de los modernos supercomputadores, un verdadero salto cualitativo en este campo sólo será posible si somos capaces de avanzar significativamente en algunos de los problemas matemáticos que describiremos en este artículo.
El reto es grande pero se confirma la oportunidad de la célebre frase de Isaac Newton según la cual “caminamos a hombros de gigantes”. En efecto, son las contribuciones de Euler y el propio Newton, entre otros, las que nos permiten entender el estado del arte y planificar la investigación futura.
2. Diseño óptimo en aeronáutica
En muchas disciplinas de ingeniería, y esencialmente en aeronáutica, el uso sistemático de los métodos matemáticos para simular y optimizar procesos tiene ya una larga tradición y resulta indispensable para ahorrar energía, reducir costes y polución y para aumentar la seguridad. Por ejemplo, no hay prototipo de nuevo automóvil de turismo que sea construido sin haber previamente recorrido millones de kilómetros en simulaciones por ordenador. A pesar de ello, aún a día de hoy, la simulación y optimización de una aeronave entera tiene un coste computacional prohibitivo.
Son varias las razones para que esto sea así y es por eso que ésta es un área en la que se continúa haciendo un esfuerzo investigador importante y en el que las Matemáticas tienen cada vez más protagonismo.
Desde un punto de vista matemático el problema se formula de la siguiente manera. El avión ocupa una región o dominio del espacio tridimensional en torno a la cual fluye el aire. Nótese que adoptamos un punto de vista más propio del de los ensayos en túneles de viento que en el vuelo real, en el que la nave está en movimiento mientras que en nuestro modelo matemático consideramos que la aeronave está fija y es el aire el que fluye en torno a la misma, lo cual nos permite trabajar en un sistema de coordenadas fijo.

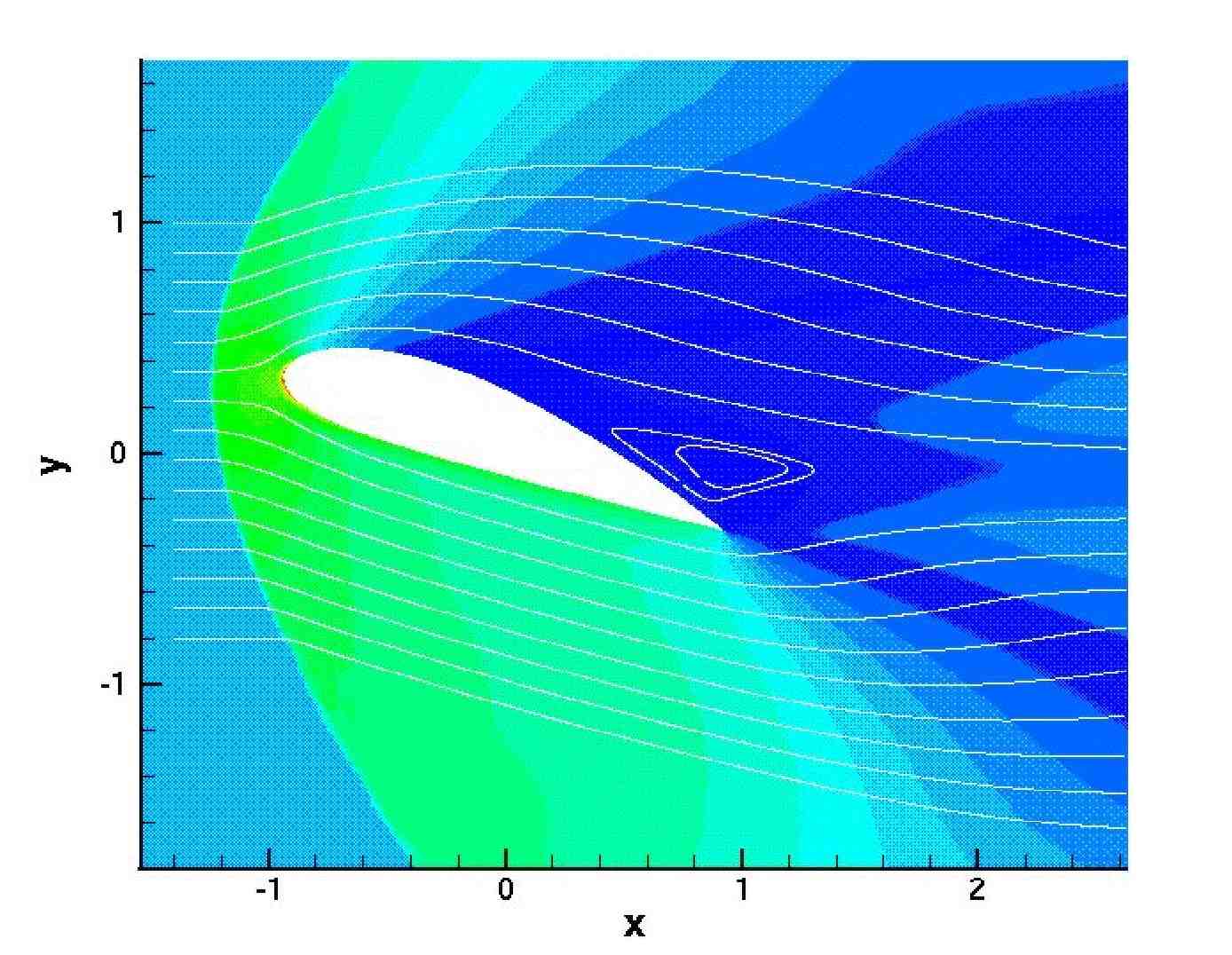
Figura 1: Forma típica de una aeronave y simulación numérica bi-dimensional del campo de presiones ejercido por el aire.
En la práctica, se pretende determinar la forma de la aeronave que optimice algún criterio de interés industrial, comercial o medioambiental. Por ejemplo, que se maximice la sustentación de la aeronave o se minimice el consumo de combustible. Con el objeto de medir estas cantidades introducimos una función o funcional de coste2 J (Ω), por ejemplo el consumo de combustible. Para simplificar un poco la presentación supongamos que buscamos un mínimo de J, lo cual es, además, un problema muy natural cuando hablamos del consumo de combustible. El problema consiste por tanto en minimizar el funcional coste en un conjunto de formas admisibles para el avión, es decir, de las posibles formas geométricas de la aeronave.
Este tipo de problemas son ubicuos en muy diversos ámbitos de la actividad humana y son los que han dado lugar al desarrollo de campos tan importantes de las Matemáticas como el Cálculo de Variaciones o la Investigación Operativa. Este último se ocupa, en particular, de problemas de planificación en las que el gran número de parámetros hace imposible una solución basada en la mera intuición (planificación del funcionamiento de los semáforos de una gran ciudad, por ejemplo, o distribución de personal en una gran empresa, con diversos departamentos y turnos.)
Volviendo al caso de la aeronáutica que nos ocupa, una de las principales dificultades radica frecuentemente en la complejidad del funcional coste en consideración, que depende de la forma de la aeronave de manera muy poco evidente, a través del campo de velocidades del fluido que lo rodea (el aire).
Es por eso que una de las piezas clave de la metodología matemática que aquí describimos es disponer de modelos fiables para el comportamiento del aire entorno al diseño en consideración y de métodos computacionales aproximados para su cálculo y previsión. Este es precisamente el papel de la Mecánica de Fluidos que proporciona diversos modelos que permiten identificar el campo de velocidades del fluido (que indica esencialmente en qué dirección y con qué velocidad se mueve cada partícula de fluido) a través de sistemas de Ecuaciones en Derivadas Parciales (EDP) que describen el movimiento del aire en torno a la aeronave.
Hay toda una jerarquía de tales modelos dependiendo de que consideremos un modelo tridimensional completo que evoluciona en el tiempo, estacionario (independiente del tiempo), que tengamos en cuenta los efectos de la viscosidad del aire o no, de la turbulencia que se genera en torno a la aeronave, que adoptemos un modelo reducido bi o uni-dimensional, etc. Entre ellos cabe destacar las ecuaciones de Navier-Stokes, las de Euler, los modelos de turbulencia (Reynolds-Averaged Navier-Stokes (RANS), el modelo de Spalart-Allmaras) y las ecuaciones de Burgers.
Como estamos viendo, todo esto es un proceso complejo en el que intervienen diferentes ingredientes de las más diversas áreas: Mecánica de Fluidos, Ecuaciones en Derivadas Parciales, Diseño óptimo, Geometría,… Sería materialmente imposible concluir con éxito este programa sin la ayuda del Análisis y la Simulación Numérica mediante los ordenadores más potentes.
En este punto conviene también que tengamos en cuenta que, a pesar de que en cada uno de los pasos que debemos dar en el desarrollo de este ambicioso programa usemos los métodos computacionales más eficaces, el pequeño error computacional que cometamos en cada paso puede tener un efecto acumulado importante en el resultado final. Obviamente, en la práctica, el diseño óptimo nunca se alcanza, ni es imprescindible hacerlo pues una mejora significativa del diseño previo suele resultar rentable y suficiente. Ahora bien, sólo la combinación de las herramientas más punteras existentes y el diseño de nuevos métodos matemáticos y computacionales puede dar lugar a una mejora de los diseños ya existentes incluso si el objetivo final es la mejora de su rendimiento en un porcentaje aparentemente pequeño.
El punto de vista que adoptamos al abordar el diseño de las aeronaves desde las Matemáticas es aquél, según el cual, al alterarse la forma de la aeronave en búsqueda del óptimo, se altera el flujo del fluido, el aire en este caso, a su alrededor. Es la interacción del cuerpo del avión con el aire la que determina el grado eficacia del diseño, a través del valor correspondiente del funcional de coste, que normalmente está definido sobre la superficie exterior de la aeronave (lo que en Matemáticas se denomina frontera) y que mide cantidades físicas que afectan el rendimiento del avión, como la resistencia, la presión o la sustentación de dicha configuración.
3. Los métodos de descenso
La mayoría de los métodos computacionales que se desarrollan en el ámbito de la Matemática Aplicada son de carácter iterativo. Es el caso de los métodos de descenso que describimos en esta sección. El principio básico es tan sencillo y natural como eficaz y reposa en el hecho de que, si somos capaces de encontrar un método que mejore un diseño previo, aplicando este método de manera reiterada, deberíamos obtener diseños cada vez mejores, del mismo modo que la práctica constante en cualquier actividad nos permite mejorar el rendimiento.
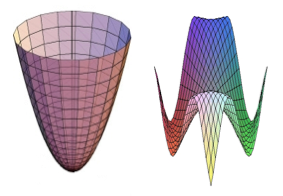
Figura 2: Izquierda: Superficie de un parabolide cuyo mínimo está bien identificado y que un método de descenso encuentra con facilidad. Derecha: Superfecie más compleja en la que los métodos de descenso corren el riesgo de no converger.
Suponiendo que hayamos ya solventado el problema de obtener una aproximación adecuada del campo de velocidades del fluido, lo cual a su vez permite un cálculo efectivo fiable del valor del funcional coste en una determinada configuración geométrica nos enfrentamos ahora a la minimización del funcional coste en consideración.
Veamos cómo podemos diseñar un método iterativo que pueda ser de utilización sistemática en la minimización de funcionales y por tanto en diseño óptimo.
En aquellos casos en que el funcional es convexo que se emplea para denominar las figuras que presentan la forma que se indica en la izquierda de la Figura.
En cualquier caso, lo que debemos mantener en mente es que los métodos de descenso que vamos a describir funcionan y proporcionan el valor mínimo en aquellas situaciones geométricas en las que una partícula depositada sobre la superficie y sometida a la fuerza de la gravedad converge.
Tal y como se muestra en la izquierda de la Figura, es relativamente fácil calcular su mínimo a través de un método iterativo de descenso que lo que hace es reproducir algorítmicamente la trayectoria que una canica en el interior de la superficie seguiría hasta caer en el punto de mínimo por efecto de la gravedad, o la que adoptaríamos para descender una ladera lo más rápido posible.
Desafortunadamente, en las aplicaciones aeronáuticas que nos ocupan, a causa de la compleja dependencia del funcional con respecto al dominio a través de las ecuaciones de la Mecánica de Fluidos antes mencionadas, no podemos asegurar que se tenga la forma convexa que tanto conviene a los métodos iterativos de minimización (véase la figura de la izquierda más abajo), sino más bien todo lo contrario, presentándose más bien una gráfica como la mostrada a la derecha.
Recordemos brevemente el algoritmo iterativo del método de gradiente, también denominado, muy elocuentemente, de máxima pendiente o “steepest descent” que reproduce precisamente la dinámica de la canica sometida a la fuerza de la gravedad a la que antes hacíamos alusión. En este punto y en lo sucesivo abusamos de la notación. Para dar un sentido riguroso a estas fórmulas deberíamos considerar el funcional definido en un espacio de Hilbert, definir la distancia entre dominios, sus deformaciones a través de campos que apunten en la dirección normal, etc. Se dispone una teoría matemática consistente que arranca en los trabajos de J. Hadamard y que permite dar rigor a todo lo que aquí describimos.
En ausencia de convexidad, como en la figura de la izquierda más arriba, es fácil imaginar cómo una canica ubicada en la gráfica se perdería en una dinámica ininterrumpida sobre la superficie con esta geometría compleja, por efecto de la gravedad, sin nunca llegar a un punto de mínimo.
Pero, en la práctica, a pesar de no poder garantizar que estemos en una configuración en la que el mínimo del funcional existe, este hecho no es un obstáculo para seguir aplicando la metodología que estamos presentando, puesto que, como habíamos visto anteriormente, lo que realmente se busca en una aplicación, es una nueva configuración que mejore la anterior.
El método consiste en, a partir de un diseño inicial de arrancada producir la sucesión de diseños, de modo que, en cada paso, deforme el dominio previo en la dirección de máximo descenso del funcional coste.
Hay otras versiones y variantes de este método de máximo descenso como el método de gradiente conjugado, el de Newton, etc. que son más eficaces pero que están inspirados en el mismo tipo de ideas y que, en definitiva, producen una sucesión que aproxima el mínimo que supone una variante de la anterior.
La aplicación de los métodos iterativos, tal y como el método del gradiente, necesitan, en cada paso de la iteración, calcular el gradiente del funcional a minimizar que representa la sensibilidad del funcional con respecto a cada uno de los parámetros de diseño. Es un principio fundamental que una buena estrategia de optimización ha de estar basada en una buena comprensión del funcional a minimizar, lo mismo que el pilotaje de un vehículo con destreza exige un buen conocimiento de la respuesta del mismo al accionamiento de los diversos mandos que lo regulan. El gradiente codifica precisamente la sensibilidad del funcional frente a la alteración de los parámetros de diseño.
El cálculo del gradiente, como vamos a ver, es formalmente fácil de realizar aunque, cuando abordamos las aplicaciones reales a las que nos referimos, puede resultar sumamente costoso y complejo cuando el número de parámetros de diseño es elevado. Por ejemplo, en el ámbito del diseño de una aeronave el número de parámetros relevantes puede ser del orden del centenar, correspondiendo cada uno de ellos a diferentes elementos geométricos de la aeronave (alas, sustentadores, cola, motores, etc.) sin contar otros como los propios materiales de los que está constituida, tema de gran actualidad también en el mundo de la aeronáutica que comienza a incorporar nuevos materiales en sus modelos más vanguardistas.
En la práctica, el campo fluido obedece a las ecuaciones de la Mecánica de Fluidos en el exterior de la región ocupada por la aeronave. Al derivar estas ecuaciones con respecto a las deformaciones del dominio, con el objeto de calcular la sensibilidad del fluido con respecto a variaciones de la misma, se obtiene un modelo linealizado, a las ecuaciones no-lineales que gobiernan el comportamiento del propio campo fluido.
Esto supone un gran inconveniente cuando consideramos problemas en los que el número de parámetros de diseño es muy grande, como ocurre en la práctica. En efecto, en una aplicación real, la ecuación de fluidos no puede ser resuelta analíticamente sino que ha de ser aproximada numéricamente.
En la práctica estas ecuaciones han de resolverse de manera aproximada mediante el uso de herramientas computacionales gracias a los ordenadores, discretizando el dominio fluido, y generando un mallado computacional. Cada nodo de este mallado es un punto en el que aproximamos la solución.

Figura 3: Izquierda: Mallado o triangulación del dominio computacional constituido por el exterior de una sección bidimensional de un ala. Centro: Mallado regular del plano. Derecha: Deformaciones de Hicks-Henne en el diseño de la sección 2-d de un ala.
Antes hablábamos del gran número de parámetros de diseño que se presentan habitualmente en las aplicaciones. En principio, a nivel computacional, la deformación de la geometría podría realizarse moviendo cada nodo que está sobre su superficie, pero esto sería inmanejable. En la práctica no es esto lo que se hace sino que se identifican zonas o perfiles que deforman simultáneamente un cierto número de nodos, con unas formas predeterminadas, fruto de desarrollos analíticos o experimentales. Pero, a pesar de ello, el número de parámetros de diseño resulta aún del orden de las decenas y esto tiene un coste computacional excesivo.
Esto puede ser remediado por la técnica del “estado adjunto” que constituye una versión moderna de los clásicos multiplicadores de Lagrange que nos permite, mediante la resolución de un sólo sistema adicional, calcular la sensibilidad con respecto a cualquier parámetro.
4. Las matemáticas de los fluidos
Los modelos matemáticos de los fluidos son algunos de los objetos matemáticos más complejos y relevantes sobre los que aún no se dispone una comprensión completa. Son muchos los factores que hacen que esto sea así. Uno de ellos es el hecho de que las soluciones desarrollen choques o discontinuidades, del mismo modo que las olas marinas se rompen al llegar al litoral. Esto hace que los métodos matemáticos habituales, basados en la intuición y técnicas desarrolladas en el ámbito de las superficies y funciones regulares, y que conducen a los gradientes de los funcionales que hemos de emplear en la implementación de los métodos de descenso, no puedan ser utilizados sin una revisión a fondo de los mismos.
Los choques o singularidades en Mecánica de Fluidos son un tema clásico y sin duda uno de los más importantes para la teoría actual de EDP. Por otra parte, las ondas de choque son de hecho uno de los fenómenos más relevantes en muy diversos ámbitos de la Mecánica (detonaciones, terremotos, fracturas, etc.) y, como vamos a ver, influyen de manera decisiva en los diseños aeronáuticos.
Desde un punto de vista matemático, sin ir más lejos, la unicidad y regularidad de las soluciones de las ecuaciones de Navier-Stokes en tres dimensiones espaciales constituye uno de los problemas del milenio de la Fundación Clay.
El modelo más sencillo en el que este tipo de fenómenos queda de manifiesto es la ecuación de Burgers uni-dimensional que se asemeja a las ecuaciones de Euler de los fluidos perfectos en tres dimensiones espaciales. Sus soluciones desarrollan discontinuidades, también denominadas choques, de igual modo que las olas del mar, con perfiles suaves en alta mar, se rompen al llegar a la costa. Esto es así pues las soluciones toman valores constantes a lo largo de las trayectorias que describen las denominadas curvas características que son las que trazan las propias partículas del fluido en movimiento. Al colisionar dos partículas las soluciones se encuentran ante el conflicto de tomar dos valores distintos, generando una discontinuidad, del mismo modo que el tubo de una ola, antes de romperse, se enrolla sobre sí mismo en una configuración aparentemente imposible.
Tal y como hemos señalado, uno de los elementos clave en el desarrollo de la metodología que acabamos de presentar, es la utilización de esquemas numéricos eficaces para la aproximación de las soluciones puesto que éstas rara vez pueden ser obtenidas de forma explícita.
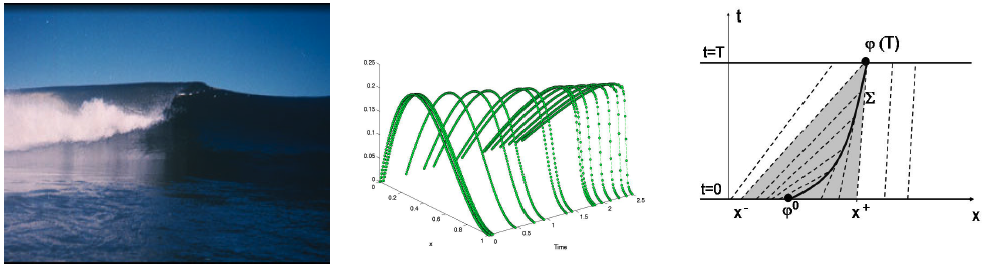
Figura 4: Izquierda: Imagen de una ola que en su lado izquierdo ya se ha roto y que en el otro está a punto de hacerlo. Centro: Evolución de un frente solución de la ecuación de Burgers sin viscosidad que, de izquierda a derecah, se observa como desarrolla un choque. Derecha: Recas características que colisionan describiendo una curva sobre la que se propaga un choque.
En el marco de la ecuación de Burgers, en ausencia de viscosidad, los esquemas más habituales son esquemas en diferencias finitas conservativos.
Existen muchos esquemas numéricos que satisfacen las condiciones de consistencia y estabilidad necesarias para garantizar su convergencia (Lax-Friedrichs, Engquist-Osher, Godunov, Roe, etc.) y se distinguen, en particular, por tener una eficacia muy distinta cuando se trata de aproximar soluciones que presentan choques.
Frecuentemente, los esquemas más eficaces, como el de Godunov y Roe, no son diferenciables, al involucrar una función de flujo que no lo es lo cual impide la aplicación de los métodos de descenso basados en el gradiente del funcional, tal y como los hemos presentado.
En efecto, la posible presencia de discontinuidades o choques en las soluciones hace que los esquemas tengan que ser sensibles al direccionamiento del flujo e incluso a su amplitud. Esto hace que todo buen esquema haya de incorporar limitadores, términos que se activan sólo en determinadas circunstancias en función del valor de ciertos sensores que miden, en particular, la inminencia de los posibles choques. De este modo los esquemas dejan de ser suaves en el paso de un nodo a otro y el formalismo de linealización anterior deja de ser válido. Este problema es inevitable pues los esquemas suaves, para capturar los choques de las soluciones, necesitan unos mallados tan finos que en la práctica suponen un coste computacional excesivo y no pueden ser utilizados.
Esto conduce a un difícil dilema: Necesitamos esquemas que resuelvan bien los posibles choques que se presentan en el fluido, pero esto nos obliga a utilizar esquemas numéricos que no son diferenciables, lo cual dificulta considerablemente el empleo de los métodos de descenso.
Se trata éste de un tema de gran importancia, que se acrecienta en problemas más complejos derivados de las aplicaciones a la aeronáutica que describimos y que son objeto aún de investigaciones exhaustivas.
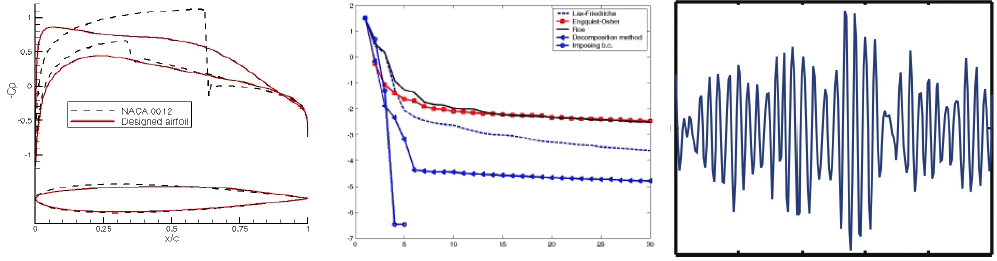
Figura 5: Izquierda: Evolución del coeficiente de presiones Cp a lo larago de la superficie del ala, al pasar de la geometría incial (en negro) a la nueva (en rojo) tras un proceso de optimizacón. Centro: Rendimiento de los diversos métodos de descenso aplicados a la ecuación de Burgers mediante diferentes esquemas de discretización y diferenciando, sobre todo, el tratamiento de los choques. Derecha: Inestabilidades numéricas.
Una vez de haber desarrollado el programa matemático expuesto y el algoritmo de descenso en alguno de los lenguajes de programación más avanzados, pondremos el programa en marcha en el ordenador (normalmente un superordenador o granja de ordenadores para simulaciones de características realistas) a la espera de obtener un diseño algo mejor que el que teníamos anteriormente.
Pero no hay que excluir que nos encontremos, de manera inesperada y contrariamente a nuestras expectativas, con resultados un tanto desconcertantes. En efecto, es frecuente que cuando, al cabo de un gran número de iteraciones y de haber consumido el tiempo computacional disponible, paramos un algoritmo, observar un resultado fuertemente oscilante que resulte a todas luces inutilizable puesto que una deformación de este tipo de la forma de un vehículo es irrealizable y contraria al propio sentido común.
Estamos frente a una falsa solución, espuria, producida por el método numérico, un fantasma numérico, y no la que corresponde al problema real original planteado. Es una situación producida por la acumulación de errores numéricos que en los que en cada paso del complejo proceso de optimización vamos incurriendo y que acaban corrompiendo completamente los resultados numéricos finales. Es una manifestación de haber violado la condición de estabilidad que, junto con la de consistencia antes mencionada, según el Teorema de Peter Lax (Premio Abel 2005), garantiza la convergencia de un método numérico. Esta inestabilidad es la que produce este tipo de resultado altamente oscilante, de alta frecuencia y gran amplitud.
Es por eso que los algoritmos iterativos de tipo gradiente que hemos descrito han de ser suplementados con frecuencia con técnicas de filtrado y/ o regularización de las altas frecuencias espurias, lo cual se realiza con frecuencia mediante la utilización de varios mallados simultáneos, del mismo modo que las obras de arte necesitan de un acabado o pulido final antes de considerarse terminadas.
Conclusiones: Algunos retos
En este artículo hemos descrito los ingredientes principales de los métodos matemáticos de Diseño óptimo de formas, centrándonos en la aeronáutica. Como hemos visto, son muy diversos los elementos que intervienen en el desarrollo de una metodología global y sistemática y en la que las Matemáticas juegan un papel central, en coordinación con otras disciplinas y muy en particular con la Computación.
El programa que hemos descrito está fuertemente inspirado en las ideas de algunos de los clásicos como Euler y Newton, pero utiliza los desarrollos más actuales y avanzados de muy diversos ámbitos de las Matemáticas. Hemos mencionado las dificultades que surgen en su implementación y algunos problemas abiertos a los que esto conduce, que son de profundo calado matemático. En esta última sección realizamos un breve resumen de las principales problemas abiertos que se plantean en éste área, no sin antes recordar que la metodología descrita tiene un carácter universal por su amplio e importante espectro de aplicaciones al que aludíamos al inicio de este artículo, más allá de los propios de la aeronáutica.
Pero, afortunadamente, caminamos a hombros de gigantes!
Entre los problemas más relevantes que quedan por resolver en este campo cabe mencionar:
• Regularidad y unicidad de las soluciones de las ecuaciones de los fluidos en tres dimensiones espaciales.
• Desarrollo de métodos de identificación de choques y singularidades, lo cuál requerirá el empleo y desarrollo de técnicas propias del tratamiento de imágenes y de la geometría computacional.
• Análisis de la sensibilidad de los funcionales de coste habituales con respecto a las singularidades del fluido.
• Métodos eficaces para resolver numéricamente las ecuaciones adjuntas que, aunque tengan un aspecto semejante a los modelos clásicos de la Mecánica de Fluidos, poseen soluciones con características muy distintas a las ecuaciones de estado que no son fáciles de capturar.
• Desarrollo de nuevos métodos de minimización, que transciendan los métodos gradiente habituales, puesto que estos últimos permiten mejorar los diseños ya existentes pero no dar con otros más innovadores.
• Desarrollo de métodos de filtrado y regularización de las oscilaciones espurias que funcionen de manera sistemática y de modo que el calibrado de los parámetros relevantes pueda automatizarse.
Todos estos problemas técnicos se enmarcan en un esfuerzo colectivo, que necesita un abordaje multidisciplinar, y que tiene como objetivo último el desarrollo de métodos computacionales integrados en los que los procesos de simulación del fluido y la optimización se realicen en paralelo, proporcionando herramientas de diseño que puedan ser usados de manera intuitiva, creativa, versátil y en tiempo real en entornos avanzados de diseño, dotados de las más modernas tecnologías, en particular, de realidad virtual.
1 Agradezco a Francisco Palacios (Universidad de Stanford) por tantos años de colaboración y todas esas conversaciones e intercambios de correos electrónicos que me han permitido conocer un poco más de este apasionante tema. Francisco es el creador de la plataforma computacional más avanzado y además de libre acceso en el campo de la simulación y diseño de formas en aeronáutica: Stanford University Unstructured (SU2); http://su2.stanford.edu/
2 Entendemos por ello que, con la capacidad de cálculo de los ordenadores actuales, el tiempo necesario para realizar el cálculo es tan largo que, en la práctica, éste resulta irrealizable o simplemente exige más tiempo del que disponemos. Es también frecuente que, cuando las simulaciones numéricas se prolongan excesivamente, las inestabilidades que introduce el propio algoritmo computacional acaben corrompiendo los resultados y los hagan finalmente inservibles.
3 La terminología “coste” en este contexto se utiliza en el sentido que, en muchas aplicaciones, el funcional a minimizar representa en efecto el coste económico que supone una determinada configuración. Minimizar el “coste”, tal y como nos proponemos aquí, es pues un objetivo natural desde un punto de vista de la rentabilidad económica.
4 Desafortunadamente hay una cierta ambigüedad en la terminología que se emplea. En efecto, mientras que en la literatura matemática avanzada éstas se denominan “convexas”, tal y como lo hacemos aquí, en cursos elementales de Matemáticas se denominan “cóncavas”.
Este artículo fue publicado originalmente en la revista CIC-Network, 2, Octubre 2007, pp. 22-28 y puede descargarse desde este enlace.

