Estamos en época estival, apropiada para el disfrute de la naturaleza. Hay quien elige la costa y el mar mientras que otros prefieren la montaña. Entre estos últimos, algunos, nuestros mendizales, deciden subir a pie hasta la cumbre, mientras que otros, los txirrindularis, prefieren la bici y los puertos de montaña. Y no es lo mismo, ni mucho menos. Las cumbres, los picos más altos, son las máximas cotas de altura mientras que los puertos de montaña se ubican lo más abajo posible. En la cumbre procuramos el máximo, en el puerto de montaña el mínimo, a condición de atravesar la cordillera para pasar de un valle al otro. Aquí, por nuestra complicada orografía, sabemos de eso.
“Nada escapa en la naturaleza a la regla de los mínimos y los máximos” solía decir el irrepetible Leonard Euler (Basilea, Suiza 1707 – San Petesburgo, Rusia, 1783). Y es así. Nos gusta disfrutar al máximo pero procurando dañar nuestra salud lo mínimo posible, lo cual es difícil pues, como se suele decir, casi todo lo que es apetecible o es pecado o engorda. Llegar rápido en coche sin riesgo de multas y con bajo consumo de gasolina. Difícil también. Buscamos la máxima seguridad para nuestras vidas y nada en la actividad humana escapa a esa regla de los extremos de Euler: el diseño, el urbanismo, el arte, la publicidad, la política,…
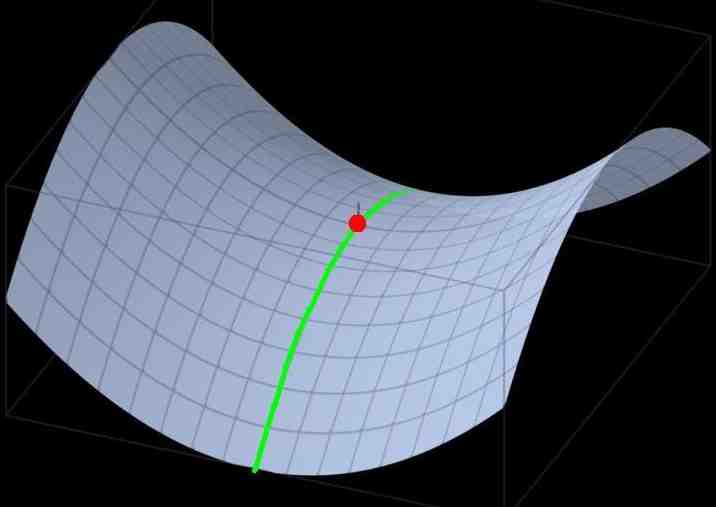
Cumbres y pasos de montaña corresponden a dos formas, a dos configuraciones geométricas bien distintas. Las primeras tienen forma de cono o campana, mientras que las segundas se parecen más a una silla de montar. De hecho en Matemáticas se les denomina puntos de ensilladura.
La silla de montar tiene esa forma curiosa que le permite adaptarse al lomo del caballo, resultando estable y lo menos incómoda posible para el jinete. De hecho, los vaqueros de las películas, a fuerza de ir montados en la ensilladura, acaban arqueando sus piernas al caminar, del mismo modo que el sofá acaba cediendo al peso persistente de nuestros cuerpos. Es el caso del héroe del comic Lucky Luke, que tiene además el privilegio de ser “más rápido que su propia sombra”, lo cual ya nos gustaría a muchos, aunque, últimamente, visto el tiempo que hace, nos conformaríamos con que luciese el sol para contemplar de nuevo nuestra sombra aunque sea estáticamente.
Las sillas de montar adoptan esa curiosa forma combinando hábilmente los mínimos y los máximos: Mínimo en la dirección del lomo del caballo, máximo para las piernas del jinete. Por eso, en diversos campos de la Ciencia, a esa configuración la denominamos Min-Max.
Min-Max es compromiso y equilibrio sutil. Si en nuestros mapas señala los pasos de montaña, está también en el corazón de la Teoría de Juegos, disciplina que se ocupa del análisis de procesos donde diversos agentes interactúan en escenarios complejos y de los que muchas veces suelen depender importantes decisiones estratégicas en materia económica, social, bélica, geopolítica,…
Los periódicos todos los días dan cuenta de numerosos ejemplos. Sin ir más lejos, estos días, nos narran las dudas de Wert sobre la nota que va a ser necesaria para alcanzar una beca de estudios. Un paso adelante, otro atrás, manifestaciones, protestas, reuniones, negociaciones. Se trata en definitiva de llegar a ese punto de Min-Max de satisfacción razonable para ambas partes, interesadas en resultados opuestos: que la nota de corte suba (Max) por parte del Ministerio y que baje (Min) por alumnos y familias. Se debate también sobre el nivel de impuestos que los ciudadanos debemos pagar sabiendo que a más impuestos (Max), más dinero disponible en las arcas públicas, pero también el riesgo de una contracción del consumo con lo que eso supone de bajón (Min) en la actividad económica. Se trata en ambos casos de juegos no cooperativos pues los diversos agentes implicados buscan resultados opuestos: lo que uno gana lo pierde el otro. Y no son precisamente juegos de los más infantiles, lúdicos e inofensivos.
Las Matemáticas siempre se han ocupado de este importante tema pues sólo a través de ellas se puede calcular cuál es la mejor solución posible para cada jugador y así desplegar la estrategia más hábil. Y esto no siempre es fácil pues, en gran medida, depende del tipo de juego, del número de jugadores, de su personalidad, de cuál sea su objetivo último, de si es esperable la cooperación entre ellos, de hasta qué nivel de riesgo vaya a asumir cada uno, de sus valores éticos,…
La existencia o no de cooperación es una de las claves que determinan la mecánica del juego. El juego del mus es un buen ejemplo: Dos parejas compiten con intereses opuestos, pero los miembros de cada una de ellas cooperan. Y de la habilidad en esa cooperación depende en gran medida el resultado.
Euskadi ha sido un modelo de cooperación en muchos ámbitos, incluido el económico e industrial. Hoy sabemos que cooperando se puede crear más riqueza y también hacer frente de manera más solidaria a las situaciones de crisis. Pero los tiempos cambian, la globalización avanza y, desafortunadamente, los juegos no cooperativos invaden con demasiada frecuencia ámbitos en los que hasta ahora predominaba la cooperación. Es por eso que estamos también ante una crisis de valores, porque hemos empezado a jugar distinto.
La película “Una mente maravillosa” (2001) que nos narra la biografía del genial y esquizofrénico matemático americano John Nash (1928-) ilustra el momento en que el protagonista, Premio Nobel de Economía en 1994, da con su Teorema sobre los juegos no cooperativos. Sí, siendo matemático ganó el Premio en el área de la Economía en un campo como la Teoría de Juegos, fértil terreno común en la intersección de ambas disciplinas.
Según Nash el equilibrio se produce cuando cada jugador no puede mejorar su elección en función de la de los demás, como cuando los niños se apresuran a recoger los caramelos que lanza Olentzero en su paseo anual por la ciudad. En ese equilibrio nadie queda del todo satisfecho pero se puede consolar pensando que no podría haber hecho más en aquellas circunstancias. Podrían colaborar, organizarse para recoger todos los caramelos con cuidado y repartirlos al final, pero la ilusión les empuja a correr y competir por recoger cada uno el máximo posible, pisoteando unos cuantos. Lo mismo ocurre al desalojar grandes espacios públicos en situaciones de emergencia, por ejemplo.
John Nash es hoy, a sus 85 años, uno de los más genuinos representantes en vida de la genialidad matemática. A pesar de los prolongados períodos en los que se encontró en fuera de juego por sus problemas psiquiátricos, fue capaz de contribuir de manera decisiva en disciplinas matemáticas muy variadas. Y, en su excentricidad, nos dejó también algunas frases memorables, como cuando dijo haberse dado cuenta de que ya estaba psiquiátricamente mejor cuando dejó de pensar en clave política para hacerlo como un verdadero científico. Un poco injusto tal vez habida cuenta de que los políticos son grandes consumidores de sus teorías aunque, vista la crisis global en las que estamos inmersos, parece que más de uno ha interpretado mal su famoso Teorema.
Este verano toca poco sol y poca sombra para los que nos quedamos por aquí y para desgracia de Lucky Luke. Los que elijan montaña practicarán el Min-Max y a quienes tienen la responsabilidad de dirigir Europa les pediremos que sigan trabajando el Teorema de Nash para que encuentren la puerta de salida a la compleja encrucijada socioeconómica en la que nos encontramos, que parece más de Min-Min que de Min-Max. Nosotros estamos dispuestos a jugar cooperativamente.