Uhinez inguraturik bizi gara baina ez gara ohartzen!
Centro Nacional de Matemáticas
La proliferación de universidades ha contribuido a la atomización de equipos de investigación contrariamente a los intentos de aunar esfuerzos y equipos de los diferentes Planes Nacionales en las convocatorias anuales de proyectos.
MATEMATIKAK
Turnpike Control and Deep Learning
Matematikarien lana askotan lur azpikoa izaten da
Gaur egungo injeniaritza, zientzia eta teknika guztietako mekanismo gehienek badaukate kontrolaren aspektoren bat, automatizazioaren beharra eta abar.
Fluidoen mekanikaren erronkak nontzagai BCAMen
El parque tecnológico de Bizkaia acogió un seminario sobre los “Desafíos de la dinámica de fluidos”, un campo de la matemática que trata de resolver algunos de los retos que se presentan en áreas como el cálculo o la aeronáutica.
Propagation, dispersion, control and numerical approximation of waves
“No soy un héroe de las matemáticas. Por eso no quiero que todo el mundo me esté mirando”. Grigori Perelman.
¿Qué son las matemáticas?
Las matemáticas junto con el lenguaje son, probablemente, los principales ladrillos de una sociedad moderna y la más compleja y bella construcción de la humanidad.
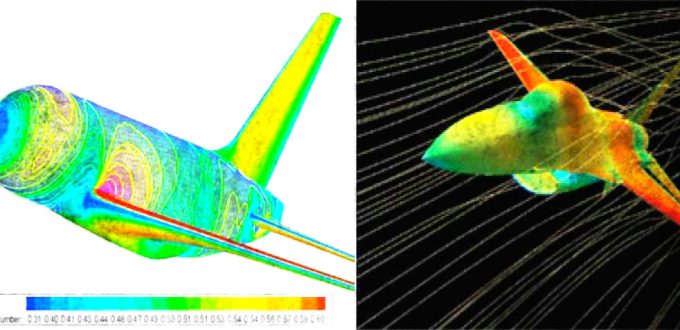
Flow control in the presence of shocks
El Institut national de recherche en sciences et technologies du numérique (INRIA) acogió en mayo de 2008 la conferencia de Enrique Zuazua titulada “Flow control in the presence of shocks. Le modèle et l’algorithme”.
Ondas continuas y discretas
La ecuación de ondas ha sido uno de los protagonistas más destacados de las matemáticas de estos últimos dos siglos.