Hay dos aspectos sorprendentes del origen, historia y estado actual de las matemáticas que son objeto de debate recurrente. El primero es la increíble capacidad de las matemáticas para describir procesos naturales, industriales y tecnológicos, mientras que el segundo se refiere a la unidad e interconexión de todas las disciplinas matemáticas.
Como ejemplo de estas dos características intrínsecas de las matemáticas, en este artículo describiremos algunas de las pasarelas que unen dos de sus ramas: la teoría de control y el aprendizaje automático (AA). Como vamos a ver, estas áreas, ambas de gran impacto tecnológico, constituyen valles vecinos en el complejo paisaje del universo matemático. En particular, la teoría del control forma parte indiscutible y relevante de los cimientos del AA.
Aristóteles se anticipó cuando apuntó a la necesidad de que los procesos se automatizaran para liberar a los seres humanos de sus tareas más pesadas, [3]. Dos milenios más tarde, en la década de 1940, el matemático y filósofo Norbert Wiener redefinió el término “cibernética” -que anteriormente había acuñado André-Marie Ampère– como “la ciencia de la comunicación y el control en animales y máquinas”.
La definición de Wiener refleja la contribución definitiva realizada por la disciplina del control / cibernética a la revolución industrial e involucra dos binomios conceptuales esenciales. El primero es el de “control-comunicación”, subrayando la necesidad de información suficiente y de calidad sobre el estado de un sistema para tomar las decisiones correctas, alcanzar un objetivo determinado o evitar que el sistema entre en regímenes de riesgo. El segundo binomio es el de “animal-máquina” que refleja el empeño humano, predicho por Aristóteles, de construir máquinas que realicen tareas que, de otro modo, les impedirían dedicar tiempo y energía a otras más satisfactorias.
Por otra parte, el desarrollo de máquinas que “aprendan” es el objetivo principal del aprendizaje automático. El estrecho vínculo entre el control y/o la cibernética y la AA se establece por tanto en la propia definición de Wiener.
Las distintas disciplinas matemáticas están divididas por cordilleras conceptuales y técnicas y a menudo han evolucionado en comunidades diferentes. Como tales, a menudo las interconexiones son difíciles de observar. Construir los caminos de conexión e identificar los hipotéticos pasos de montaña requiere un importante nivel de abstracción. Demos por tanto un paso atrás y adoptemos una perspectiva más amplia para analizar con más detalle los vínculos existentes entre el control y el AA.
La noción de controlabilidad nos ayuda a desvelar una de las pasarelas entre estas dos disciplinas. El problema de la controlabilidad consiste en conducir un sistema dinámico desde una configuración inicial a otra final en un horizonte temporal determinado mediante controles viables y hábilmente diseñados. En el marco de los sistemas lineales de dimensión finita
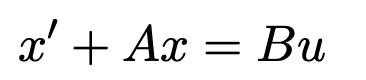
la respuesta es elemental y clásica (se remonta al trabajo de Rudolf Kalman en la década de 1950, al menos), [6]. El sistema es controlable si y sólo si la matriz que gobierna la dinámica del sistema y la que describe los efectos de los controles sobre los distintos componentes del estado verifican la célebre condición de rango
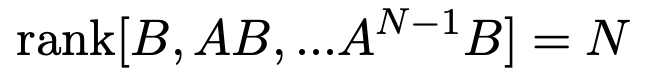
El tamaño del control depende naturalmente de la longitud del horizonte temporal; más grande horizontes temporales cortos y de menor amplitud para horizontes más largos.
![Figura 1. Control simultáneo de trayectorias de una ecuación diferencial ordinaria neuronal (NODE) para la clasificaciónsegún dos etiquetas diferentes (azul/rojo), exhibiendo la naturaleza de giro de las trayectorias. Figura cortesía de [5].](https://cmc.deusto.eus/enzuazua/wp-content/uploads/2023/05/Pic_1.png)
Figura 1. Control simultáneo de trayectorias de una ecuación diferencial ordinaria neuronal (NODE) para la clasificación
según dos etiquetas diferentes (azul/rojo), exhibiendo la naturaleza de giro de las trayectorias. Figura cortesía de [5].
¿Son estas ideas y métodos relevantes para el AA? Empecemos analizando el resultado seminal de George Cybenko: el llamado teorema de aproximación universal (TAU). El TAU afirma que una combinación finita de funciones de activación reescaladas y desplazadas (es decir, redes neuronales) de la forma 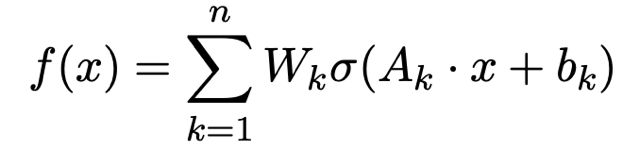
son densas en una variedad de espacios funcionales [1]. Este resultado del análisis funcional complementa otros resultados fundamentales del análisis, como la densidad de polinomios, series de Fourier y funciones suaves con soporte compacto.
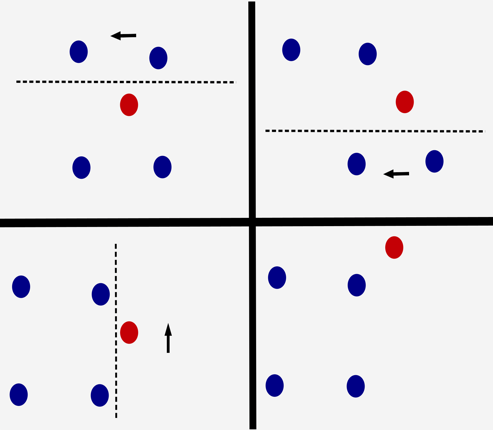
Figura 2. Movimiento canónico iterativo que conduce a la clasificación por inducción con controles de conmutación, constantes a trozos (Domènec Ruíz-Balet, Imperial College, Reino Unido).
El TAU sirve para fines de regresión y clasificación en el contexto del aprendizaje supervisado (AS). A grandes rasgos, podemos clasificar cualquier conjunto de datos simplemente aproximando la función característica -que toma valor 1 en un conjunto de elementos y 0 en el complementario- para, en última instancia, asignar la etiqueta correcta a cada elemento.
El hermoso resultado de Cybenko, demostrado empleando el teorema de Hahn-Banach, abrió la puerta a una serie de métodos que ahora desempeñan un papel esencial en el AA. En la práctica, dado que el TAU garantiza la consecución de todos los objetivos simplemente identificando los parámetros correctos en el ansatz de Cybenko, podemos adoptar el punto de vista de los mínimos cuadrados y buscar los valores de los parámetros que minimicen la distancia a la función necesaria durante la llamada fase de entrenamiento. Por supuesto, un enfoque tan ingenuo y natural conlleva grandes retos – ¡debemos enfrentarnos simultáneamente al diablo de la falta de convexidad y a la maldición de la dimensionalidad!
Eduardo Sontag y Héctor Sussmann exploraron el potencial de combinar de la teoría del control con el TAU, un esfuerzo retomado recientemente por la comunidad matemática, [2, 9]. El ansatz neural conduce ecuaciones diferenciales ordinarias neuronales (EDON)
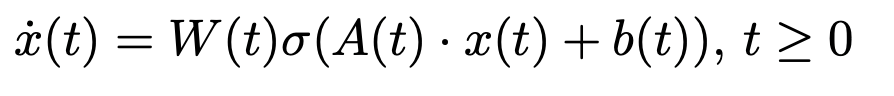
que se controlan mediante funciones de activación, como las funciones sigmoidales (funciones continuas monótonas que toman valor 0 en – y 1 en +$). Cybenko introdujo estas funciones, bastante atípicas en mecánica, con fines de aproximación.
La comunidad del control matemático tardó muchos años en comprender cómo aplicar los métodos de control a los retos reales de la AS. Trabajos recientes han demostrado por fin que las redes neuronales residuales profundas (ResNets) -discretizaciones temporales de ODENs- proporcionan la asombrosa e inesperada propiedad del control simultáneo [8]. Podemos construir controles (es decir, entrenar parámetros) de tal forma que un número arbitrariamente grande de trayectorias lleguen simultáneamente de forma casi exacta a sus objetivos: las etiquetas que corresponden a los elementos del conjunto de datos a clasificar (véase la Figura 1).
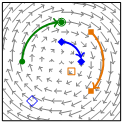
Figura 3. Movimiento generado por un sistema de control lineal. Todos los puntos se mueven simultáneamente sin posibilidad de clasificación según sus etiquetas (Daniel Veldman, FAU, Erlangen, Alemania).
Esta perspectiva de sistemas dinámicos presenta algunas ventajas interesantes al ofrecer una mejor dependencia de los datos disponibles y la oportunidad de afinar los métodos de clasificación para mejorar las propiedades de estabilidad. También puede explotar muchos de los conocimientos existentes en áreas más maduras de las matemáticas aplicadas. De hecho, la propia naturaleza de la función de activación es responsable de la propiedad excepcionalmente potente de control simultáneo que garantiza los requisitos de AS. El ejemplo más paradigmático es la función de activación de la Unidad Lineal Rectificada (ReLU), que simplemente toma el valor 0 cuando x< 0 y 1 cuando x> 0. Cuando se controla mediante la ReLU, una ODEN se comporta como un cubo de Rubik: se puede resolver mediante un número finito de operaciones inteligentes mediante las cuales parte del cubo se congela mientras la otra gira en la dirección y sentido adecuados. El objetivo de un cubo de Rubik es garantizar que todas las caras tengan un color homogéneo. Este objetivo es similar a la tarea realizada por una ODEN, que conduce cada elemento inicial a un determinado depósito distinguido según su etiqueta.
Las pruebas de las que disponemos actualmente son inductivas, mediante controles (o parámetros) constantes a trozos que permiten explotar la esencia del ReLU [8]. En cada instante de tiempo, la ReLU divide el espacio euclidiano en dos semiespacios: (i) uno que se congela a lo largo de la dinámica porque la no linealidad se anula y (ii) otro que evoluciona exponencialmente, en el que la ReLU está activa. Una elección estratégica e inductiva de los distintos hiperplanos/ecuadores (mediante la selección de los valores de los controles/parámetros) y de la dirección de la dinámica/viento (mediante el control) garantiza la clasificación en un número finito de pasos (véase la Figura 2).
Estos resultados proporcionan la teoría de base necesaria para garantizar que las ODENs cumplen las propiedades de controlabilidad simultánea que conducen a la clasificación. Por supuesto, los controles que observamos en las simulaciones numéricas suelen ser menos complejos, ya que se calculan como minimizadores de un funcional de coste convenientemente penalizado.
Conviene subrayar que estos resultados se basan fundamentalmente en la
no linealidad de las funciones de activación. De hecho, la propiedad de controlabilidad del conjunto es imposible para un sistema lineal que más bien se comportaría como el sistema de la Figura 3, incapaz de clasificar los elementos según las etiquetas.
Los resultados de control aquí presentados para ResNets y ODENs pueden trasladarse al marco de las ecuaciones de transporte (advección, convección, etc.) mediante el principio clásico de que las trayectorias de las primeras ecuaciones constituyen las características de las segundas:
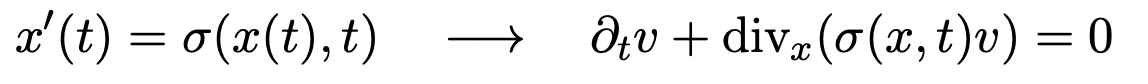
La aproximación de las distribuciones de masa a transportar mediante medidas atómicas -cuyos soportes desempeñan el papel de elementos puntuales en la clasificación- facilita esa transmutación.
De este modo el control y el AA también se unen en el problema tradicional del transporte de masas, aunque no exactamente de la misma manera que en el transporte óptimo o en el problema de Monge-Kantorovich, sino mediante campos vectoriales dependientes del tiempo con la geometría sobresimplificada que impone la función de activación.
Mis colegas y yo no somos los primeros investigadores en reivindicar las estrechas conexiones entre el control y el AA, [4, 7]. Pero ahora que llevamos varios años trabajando en este tema, nos damos cuenta de que aún queda mucho por descubrir en el vasto bosque que conecta estas dos áreas. Añadir detalles adicionales a esta íntima conexión constituirá una aportación que merece la pena al fascinante mapa global de las ciencias matemáticas.
Es probable que nuestra avance en la comprensión de estos temas siga una trayectoria en zigzag que se asemeje a las estrategias para resolver un cubo de Rubik o a las trayectorias que aseguran que las ResNets son capaces de aprender.
Hay otros ámbitos relacionados y en gran medida inexplorados que merecen también la atención de la comunidad de la matemática aplicada. Uno de ellos es el aprendizaje federado, un tema estrechamente relacionado con los métodos clásicos de splitting y descomposición de dominios del análisis numérico. Actualmente nos interesamos por este tema en colaboración con la empresa vasca de inteligencia artificial Sherpa.ai (https://www.sherpa.ai/), pero dejamos este tema para otra ocasión.
Referencias
[1] Cybenko, G. (1989). Approximation by superpositions of a single function. Math. Control Signals Syst., 2, 303-314.
[2] E, W. (2017). A proposal on machine learning via dynamical systems. Commun. Math. Stat., 5, 1-11.
[3] Fernández-Cara, E., & Zuazua, E. (2003). Control theory: History, mathematical achievements and perspectives. Bol. Soc. Esp. Mat. Apl., 26, 79-140.
[4] Fradkov, A.L. (2020). Early history of machine learning. IFAC-PapersOnLine, 53(2), 1385-1390.
[5] Geshkovski, B., & Zuazua, E. (2022). Turnpike in optimal control of PDEs, ResNets, and beyond. Acta Numer., 31, 135-263.
[6] Kalman, R.E. (1960). On the general theory of control systems. IFAC Proc. Vol., 1(1), 491-502.
[7] LeCun, Y. (1988). A theoretical framework for back-propagation. In D. Touretzky, G.E. Hinton, & T. Sejnowski (Eds.), Proceedings of the 1988 connectionist models summer school (pp. 21-28). Pittsburgh, PA: Carnegie Mellon University.
[8] Ruiz-Balet, D., & Zuazua, E. (2021). Neural ODE control for classification, approximation and transport. Preprint, arXiv:2104.05278.
[9] Sontag, E., & Sussmann, H. (1997). Complete controllability of continuous-time recurrent neural networks. Syst. Control Lett., 30(4), 177-183.
Enrique Zuazua es titular de la Cátedra de Dinámica, Control, Aprendizaje Automático y Numéric – Cátedra Alexander von Humboldt en el Departamento de Matemáticas de la Friedrich-Alexander- Universität Erlangen-Nürnberg en Alemania, que compatibiliza con una dedicación parcial en la Universidad Autónoma de Madrid y en la Fundación Deusto de Bilbao.

