Featured Video
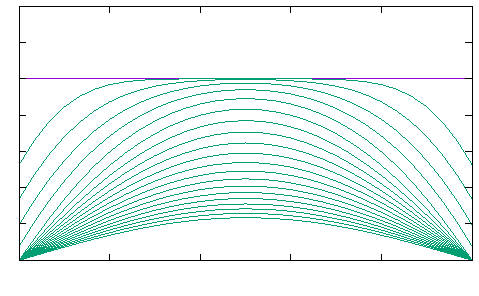
Evolution of the controls and of the state for $y^0=1$, $y^1=5$, $M=20$ and the discretization parameters $N_x=30$, $N_t=450$ in the minimal computed time $T\simeq\mathtt{0.2093}$.
Introduction
In this short tutorial we explain how to use IpOpt in order to solve time optimal control problems. We refer to [1,4,5] for a survey on numerical methods in optimal control and how to implement them efficiently according to the context.
The tools
- IpOpt is an interior-point optimization routine (see [6]).
Basically, it numerically solves optimisation problems of the form:
\begin{equation}\label{eq:P0}\tag{P0}
\begin{array}{cl}
\min & f(x)\\
\vline & \begin{array}{l}
x\in\mathbb{R}^n\, ,\\
g(x)\leqslant 0\, ,\\
h(x)=0\, .
\end{array}
\end{array}
\end{equation}
IpOpt can be used together with Matlab, FreeFem++…and can be used directly in .cpp codes. - AMPL is an automatic differentiation and the modelling language (see [2]). The interest of using AMPL together with IpOpt is that, the gradient of the cost function and the constraints is automatically generated. Solving problems with IpOpt and AMPL can be made online through the NEOS solvers.
Solving problem (P0)
Let us write in AMPL language the problem (P0).
# The variable of the problem var x {i in 1..n} # The cost function to be minimized minimize cost : f(x); # The inequality constraints subject to inequality_constraints : g(x)<=0; # The equality constraints subject to equality_constraints: h(x)=0; # Set IpOpt as solver option solver ipopt; # Set options for IpOpt, such as the maximal number of iterations option ipopt_options "max_iter=20000 linear_solver=mumps halt_on_ampl_error yes"; # Solve the problem solve; # Display the cost value printf : "# cost = %24.16e\n", cost; printf : "# Data\n"; # Display the optimal values of x printf {i in 0..n} : "%24.16e\n", x[i]; # Quit AMPL end;
Solving a time optimal control problem with constraints
Let us now turn to a time optimal control problem.
Given a dynamical system,
\begin{equation}\label{eq:1a}
\dot{y}=f(y,u)\, ,
\end{equation}
some initial condition $\mathrm{y}^0\in \mathbb{R}^n$ and some terminal condition $\mathrm{y}^1\in\mathbb{R}^n$ and some bound $M>0$, the aim is to find the minimal time $T\geqslant 0$ such that there exist a control $u\in L^\infty(0,T)^m$ such that,
\begin{equation}
|u_i(t)|\leqslant M \qquad (t\in(0,T)\ \text{a.e.}\, ,\ i\in\{1,\dots,m\}),
\end{equation}
and the solution $y$ of (1) satisfies the constraint,
\begin{equation}
g(y(t))\leqslant 0\quad (t\in(0,T)),
\end{equation}
and the terminal condition,
\begin{equation}
y(T)=\mathrm{y}^1\, ,
\end{equation}
where $g$ is given and define constraints of the state variable $y$. Of course to be able to solve this system, one needs to have $g(\mathrm{y}^0)\leqslant0$ and $g(\mathrm{y}^1)\leqslant0$.
The above optimal control problem, can be recast as an optimisation problem under constraints similar to (P0). More precisely, it is
$$\begin{array}{cl}
\min & T\\
\vline & \begin{array}{l}
u\in L^\infty(0,T)^M\, ,\\
\dot{y}=f(y,u)\, ,\quad y(0)=\mathrm{y}^0\, ,\\
y(T)=\mathrm{y}^1\, ,\\
g(y(t))\leqslant 0\qquad (t\in(0,T)).
\end{array}
\end{array}$$
In order to handle numerically, this problem, we will use a time discretization. Let us explain it with the explicit Euler method. But any other time discretization can be used.
Fix some parameter $N_t\in\mathbb{N}^*$ (the number of time steps) and for $T>0$ given, define $y_i$ the estimation of $y(iT/N_t)$ for $i\in\{0,\dots,N_t\}$. The explicit Euler scheme, gives the relation,
$$y_{i+1}=y_i+\frac{T}{N_t}f(y_i,u_i)\, ,$$
with $u_i\simeq u(iT/N_t)$. Then the state and control constraints are replaced by:
$$g(y_i)\leqslant 0 \qquad\text{and}\qquad |u_i|\leqslant M\, .$$
Consequently, in discretized version, we end up with a finite dimensional control problem under constraints, whose AMPL version is:
# Define the parameters of the problem # number of time step discretization points param Nt=100; # bound on the control param M =1; # initial condition param y0=1; # final condition param y1=0; # Define variables of the problem var y {i in 0..Nt}; # The control shall be in [-M,M] var u {i in 0..Nt} >=M, <=M; # The time T shall be nonnegative var T >=0; # The cost function is the time T minimize cost: T; # Set the constraints # y is solution of (1) subject to y_dyn {i in 0..Nt-1} : y[i+1]=y[i]+T/Nt*f(y[i],u[i]); # y(0)=y0 subject to y_init : y[0] =y0; # y(T)=y1 subject to y_end : y[Nt]=y1; # g(y(t))<=0 subject to state_constraint {i in 1..Nt-1} : g(y[i])<=0; # Solve with IpOpt option solver ipopt; option ipopt_options "max_iter=20000 linear_solver=mumps halt_on_ampl_error yes"; solve; # Display solution printf : "# T = %24.16e\n", T; printf : "# Nt = %d\n", Nt; printf : "# Data\n"; printf {i in 0..Nt} : " %24.16e\n", u[i]; printf {i in 0..Nt} : " %24.16e\n", y[i]; end;
Application to the constrained heat equation
Now we can turn to the control of the heat equation with nonnegative state constraint.
To this end, we consider the controlled 1D heat equation with Neumann boundary control.
\begin{equation}\label{eq:doc2}
\left\{
\begin{array}{r@{\>}l@{\qquad}l}
\dot{y}(t,x) & =\partial_x^2y(t,x) & (t>0\, ,\ x\in(0,1)),\\[2mm]
\partial_xy(t,0) & =v_0(t) & (t>0),\\[2mm]
\partial_xy(t,1) & =v_1(t) & (t>0),
\end{array}
\right.
\end{equation}
To this problem, we add the control constraints,
\begin{equation}\label{eq:doc2CC}
|v_0(t)|\leqslant M \quad\text{and}\quad |v_1(t)|\leqslant M\qquad (t>0\ \text{a.e.}),
\end{equation}
with some $M>0$ given and we add the state constraint,
\begin{equation}\label{eq:doc2SC}
y(t,x)\geqslant 0\qquad ( (t,x)\in \mathbb{R}_+^*\times(0,1)\ \text{a.e.}).
\end{equation}
To the system (5) we add the initial condition
\begin{equation}\label{eq:doc2IC}
y(0,x)=y^0(x)\qquad (x\in(0,1)),
\end{equation}
and the terminal condition
\begin{equation}\label{eq:doc2TC}
y(T,x)=y^1(x)\qquad (x\in(0,1)).
\end{equation}
In [3], it has been proved that every positive constant state $\mathrm{y}^0$ can be steered to some over positive constant state $\mathrm{y}^1$ in a large enough time $T$. Our goal here is to find numerically the minimal time $T$ such there exist controls satisfying (6) such that the corresponding solution $y$ of (5) and (8) satisfies the constraint (6) and the terminal condition (9), i.e.~ we aim to minimize
$$\begin{array}{cl}
\min & T\\
\vline & \begin{array}{l}
T>0\, ,\\
v_0,\, v_1\in L^\infty(0,T)\, ,
y \text{ solution of (5) and (8) satisfies}\\
\qquad y(T,\cdot)=y^1\quad \text{and}\quad y(t,x)\geqslant 0\qquad (t>0,\ x\in(0,1)\ $\text{a.e.}$).
\end{array}
\end{array}$$
Firstly, we will use a space discretization to reduce the system (5). To this end, we define $N\in\mathbb{N}^*$ and for every $n\in\{0,\dots,N\}$, $x_n=\frac{n}{N}$. Based on this discretization of $[0,1]$, we will discretized (5) using centered finite differences. That is to say, given $V(t)=(v_0(t)\, ,\ v_1(t))^\top$ and $Y(t)\in \mathbb{R}^{N+1}$, a vector approaching $\bigl( y(t,x_0),\ \dots,\ y(t,x_N)\bigr)^\top$, $Y$ is solution of
\begin{equation}\label{eq:doc3a}
\dot{Y}=AY+BV\qquad (t>0)\, ,
\end{equation}
with the initial condition
\begin{equation}
Y(0)=\mathrm{y}^0e_{N+1}
\end{equation}
the target state,
\begin{equation}
Y(T)=\mathrm{y}^1e_{N+1}
\end{equation}
the state constraint,
\begin{equation}
Y(t)\geqslant 0 \qquad (t>0\ \text{a.e.})
\end{equation}
and the control constraint,
\begin{equation}
|V_0(t)|\leqslant M\quad\text{and}\quad |V_1(t)|\leqslant M\qquad (t>0\ \text{a.e.})\, ,
\end{equation}
where we have set $e_{N+1}=(1,\dots,1)^\top\in\mathbb{R}^{N+1}$,
$$A=N^2\begin{pmatrix}
2 & -2 & 0 & \hdots& \hdots& \hdots& 0\\
1 & -2 & 1 & 0 & \hdots& \hdots& 0\\
0 & \ddots& \ddots& \ddots& \ddots& & \vdots\\
\vdots& \ddots& \ddots& \ddots& \ddots& \ddots& \vdots\\
\vdots& & \ddots& \ddots& \ddots& \ddots& 0\\
0 & \hdots& \hdots& 0 & 1 & -2 & 1\\
0 & \hdots& \hdots& \hdots& 0 & 2 & -2\\
\end{pmatrix}\in M_{N+1}(R)\qquad\text{and}\qquad B=2N\begin{pmatrix}
1&0\\
0&\vdots\\
\vdots&\vdots\\
\vdots&\vdots\\
\vdots&\vdots\\
\vdots&0\\
0 & 1
\end{pmatrix}\in M_{N+1,2}(\mathbb{R})\, .$$
Now we can discretize (10) using explicit Euler scheme and similarly to the previous example, we obtain an optimisation problem of finite dimension with constraints whose AMPL formulation is
# Parameters of the problem param Nx=30; # Number of space discretisation points param Nt=300; # Number of time discretisation points # One have to check a posteriori that the number of time steps is large enough so that the # CFL condition, T*Nx^2/Nt <=1/2, is satisfied param dx=1/Nx; # Space step param M =20; # Bound on the controls # Variables of the system # i stands for the time index and j for the space index var y {i in 0..Nt, j in 0..Nx} >=0; # State of the control problem # Neuman controls in 0 and 1. The controls are in [-M,M]. var v0 {i in 0..Nt} >=-M, <=M; var v1 {i in 0..Nt} >=-M, <=M; var T >=0; # Control time var dt=T/Nt; # Time step # Define the cost function minimize cost: T; # Define the constraints # y is solution of the discretize system subject to y_dyn {i in 0..Nt-1, j in 1..Nx-1}: (y[i+1,j]-y[i,j])*(dx)^2=(y[i,j-1]-2*y[i,j]+y[i,j+1])*dt; # Neuman boundary conditions in 0 and 1 subject to left_boundary {i in 1..Nt-1}: y[i,1]-y[i,0] =v0[i]*dx; subject to right_boundary {i in 1..Nt-1}: y[i,Nx]-y[i,Nx-1]=v1[i]*dx; # y(0)=y0 and y(T)=y1 subject to y_init {j in 0..Nx}: y[0,j] =5; subject to y_end {j in 0..Nx}: y[Nt,j]=1; # Solve with IpOpt option solver ipopt; option ipopt_options "max_iter=2000 linear_solver=mumps halt_on_ampl_error yes"; solve; # Write the solution in the file out.txt printf: " # T = %24.16e\n", T > out.txt; printf: " # Nx = %d\n", Nx >> out.txt; printf: " # Nt = %d\n", Nt >> out.txt; printf: " # Data\n" >> out.txt; printf {i in 0..Nt}: " %24.16e\n", v0[i] >> out.txt; printf {i in 0..Nt}: " %24.16e\n", v1[i] >> out.txt; printf {i in 0..Nt, j in 0..Nx}: " %24.16e\n", y[i,j] >> out.txt; end;
Once the file out.txt is written, it can be for instance read by Scilab with the following code
fid= mopen('out.txt','r'); // Open out.txt T = mfscanf(fid,'%s %s %s'); // Read ``# T ='' T = mfscanf(fid,'%f'); // Read value of T Nx = mfscanf(fid,'%s %s %s'); // Read ``# Nx ='' Nx = mfscanf(fid,'%d'); // Read value of Nx Nt = mfscanf(fid,'%s %s %s'); // Read ``# Nt ='' Nt = mfscanf(fid,'%d'); // Read value of Nt s = mfscanf(fid,'%s %s'); s=[]; // Read ``# Data'' v0 = mfscanf(Nt+1,fid,'%f'); v0=v0'; // Read the Nt+1 values of v0 v1 = mfscanf(Nt+1,fid,'%f'); v1=v1'; // Read the Nt+1 values of v1 y = mfscanf((Nt+1)*(Nx+1),fid,'%f'); // Read the (Nt+1)*(Nx+1) values of y mclose(fid); // Close out.txt y = matrix(y,Nx+1,Nt+1); y=y'; // Reshape y as a matrix, line i is the solution at time i/Nt x = 0:1/Nx:1; t = 0:T/Nt:T; // Define the space and time discretisations printf('time:\t%f\n',T); // Display the control time plot(t,[v0;v1]); sleep(2000); clf(); // plot controls and wait 2s plot2d(x,y(1,:),rect=[0 0 1 10]); sleep(100); // plot the initial state and wait 0.1s for i=2:1:Nt, plot(x,y(i,:),rect=[0 0 1 10]); sleep(10); // plot the state at each time instants end plot(x,y(\$,:),rect=[0 0 1 10]); // plot the final state
Based on these two codes, we obtain
- for $y^0=1$, $y^1=5$, $M=20$ and the discretization parameters $N_x=30$, $N_t=450$ the results displayed on the video:
(the minimal time obtained is $T\simeq\mathtt{0.2093}$); - for $y^0=5$, $y^1=1$, $M=800$ and the discretization parameters $N_x=30$, $N_t=450$ the results displayed on the video:
(the minimal time obtained is $T\simeq\mathtt{0.1938}$).
Similarly, we can consider the time optimal control problem,
$$\begin{array}{cl}
\min & T\\
\vline & \begin{array}{l}
T>0\, ,\\
u_0,\, u_1\in L^\infty(0,T)\\
u_0(t)\geqslant0\quad\text{and}\quad u_1(t)\geqslant 0 \qquad (t\in(0,T)\ \text{a.e.}),\\
y \text{ solution of (11) satisfies } y(T,\cdot)=y^1\, ,
\end{array}
\end{array}$$
with (11) given by,
\begin{equation}\label{eq:doc4}
\left\{\begin{array}{r@{\>}l@{\qquad}l}
\dot{y}(t,x) & =\partial_x^2y(t,x) & (t>0\, ,\ x\in(0,1)),\\[2mm]
y(t,0) & =u_0(t) & (t>0),\\[2mm]
y(t,1) & =u_1(t) & (t>0),\\[2mm]
y(0,x) & =y^0(x) & (x\in(0,1).
\end{array}\right.
\end{equation}
Numerically, we obtain
- for $y^0=5$, $y^1=1$, $M=50$ and the discretization parameters $N_x=30$, $N_t=450$ the results displayed on the video:
(the minimal time obtained is $T\simeq\mathtt{0.1931}$); - for $y^0=1$, $y^1=5$, $M=50$ and the discretization parameters $N_x=20$, $N_t=200$ the results displayed on the video:
(the minimal time obtained is $T\simeq\mathtt{0.0498}$); - for $y^0=1$, $y^1=5$, $M=3000$ and the discretization parameters $N_x=20$, $N_t=200$ the results displayed on the video:
(the minimal time obtained is $T\simeq\mathtt{0.0438}$).
Useful links
- IpOpt project: https://projects.coin-or.org/Ipopt
- AMPL project: http://ampl.com/products/ampl/
- NEOS solvers: https://neos-server.org/neos/solvers/
References
[1] J. T. Betts. Practical methods for optimal control and estimation using nonlinear programming. 2nd ed. Philadelphia, PA: Society for Industrial and Applied Mathematics (SIAM),2nd ed. edition, 2010.
[2] R. Fourer, D. M. Gay, and B. W. Kernighan. A modeling language for mathematical programming. Manage. Sci., 36(5):519–554, 1990.
[3] J. Lohéac, E. Trélat, and E. Zuazua. Minimal controllability time for the heat equation under state constraints. In preparation.
[4] E. Trélat. Contrôle optimal. Théorie et applications. Paris: Vuibert, 2005.
[5] E. Trélat. Optimal control and applications to aerospace: some results and challenges. J.Optim. Theory Appl., 154(3):713–758, 2012.
[6] A. Wächter and L. T. Biegler. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program., 106(1 (A)):25–57, 2006.