Spain 21.11.2022
Spectral inequalities for pseudo-differential operators and control theory on compact manifolds
Author: Duvan Cardona
In this post, we explain some results related to the null-controllability of diffusion models on closed manifolds, which is a problem of wide interest in control theory, and its relation with the validity of spectral inequalities for differential and pseudo-differential operators. We summarise our results as follows.
• We extend some spectral inequalities for elliptic positive pseudo-differential operators on compact manifolds (criteria are based on the symbols defined by local coordinate systems). Hörmander classes \Psi^m_{\rho,\delta}(M), 0\leq \delta \lt \rho \leq 1, \rho \geq 1-\delta. • Spectral inequalities for elliptic positive pseudo-differential operators on compact Lie groups (criteria are based on the matrix-valued symbols of operators). Hörmander classes \Psi^m_{\rho,\delta}(G), 0 \leq \delta \lt \rho \leq 1. • Applications to control theory: null-controllability for the fractional heat equation for an elliptic operator.
Below, we will explain our setting and we will give some preliminaries about the theory of pseudo-differential operators. In the end, we present our results about spectral inequalities and our applications to control theory.
1. Our setting: compact Lie groups and general manifolds without boundary
• Lie groups = manifolds with symmetries.
• compact Lie groups = are diffeomorphic to closed subgroups of \textnormal{U}(N)=\{M\in \mathbb{C}^{N\times N}:M^*=M^{-1}\} for N large enough.

• Examples: the torus \mathbb{T}^n\cong (\R/\mathbb{Z})^n, linear Lie groups (groups of matrices), \textnormal{SU}(n), \textnormal{SO}(n), etc. In particular, \textnormal{SU}(2)\cong \mathbb{S}^3; 0\leq \delta \lt \rho\leq 1. • If M is a closed, connected and simply connected, then M\cong \mathbb{S}^3. (The Poincaré conjecture proved by Perelman). Our approach induces global spectral inequalities on M for any 0\leq \delta \lt \rho\leq 1. • General compact manifolds 0\leq \delta \lt \rho\leq 1, \rho\geq 1-\delta.
2. Some preliminary information
• In the late 1980 { H. Donnelly and C. Fefferman} in their celebrated Inventiones’ paper proved the doubling property
\sup_{B(2R)}|\phi|\leq e^{C_1\lambda +C_2} \sup_{B(R)}|\phi|
(1)
for any eigenfunction of the Laplacian \Delta_g on M, that is, -\Delta_g \phi=\lambda^2 \phi, where B(2R) and B(R) represent concentric balls (associated to the geodesic distance) where the constants C_1 and C_2 are independent of R>0, and depending only on M.
• Charles Fefferman, Fields medal, 1978.
• The doubling property
\sup_{B(2R)}|\kappa|\leq e^{C_1\lambda +C_2} \sup_{B(R)}|\kappa|
(2)
remains valid for sums of eigenfunctions
\kappa=\sum_{\lambda_k\leq \lambda}a_k\phi_k\in \textnormal{span}\{\phi_k:\lambda_k^2\leq \lambda^2\}
of the positive Laplacian \Delta_g.
3. Another spectral inequality (that implies the Donnelly-Fefferman doubling property
• Let M be a compact Riemmanian manifold with (or without) smooth boundary \partial M. Let (\rho_j,\lambda_j^2) be the corresponding spectral data of the Laplacian -\Delta_g: -\Delta_g\rho_j=\lambda_j^2\rho_j. Then, for any non-empty open subset \omega\subset M, we have the loss of orthogonality estimate
\Vert \varkappa\Vert_{L^2(M)}\leq C_1e^{C_2 {\lambda}}\Vert \varkappa\Vert_{L^2(\omega)},\,\,\,\varkappa\in \textnormal{span}\{\rho_j:\lambda_j\leq \lambda\}.
(3)
Moreover, the growth constant C_1e^{C_2 {\lambda}} is sharp. This inequality was proved by Jerison-Lebeau/Lebeau-Robbiano/Lebeau-Zuazua.
4. The Lebeau-Robbiano result of the null-controllability of the heat equation
• Consequences: let { \omega} be a non-empty open subset of M. Then, the heat equation for the positive Laplacian \Delta_g
\begin{cases}u_t(x,t)+ \Delta_g u(x,t)=g(x,t)\cdot 1_\omega (x) ,& (x,t)\in M\times (0,T), \\u(0,x)=u_0,\end{cases}
is null-controllable at any time T>0, that is, for any initial condition u_0, there is an input function g\in L^2(M\times (0,T))} such that the solution to (4) vanishes in time T, that is u(x,T)=0, x\in M.
5. Some remarks
• In general pseudo-differential operators are non-local and the use of Carleman estimates, which is the analytical tool by excellence in the proof of the Lebeau-Robbiano spectral inequality and their subsequent generalisations, are not valid.
• It is natural to ask if the doubling property
\sup_{B(2R)}|\phi|\leq e^{C_1\lambda +C_2} \sup_{B(R)}|\phi|
(5)
remains valid for sums of eigenfunctions
\phi=\sum_{\lambda_k\leq \lambda}a_k\phi_k\in \textnormal{span}\{\phi_k:\lambda_k^2\leq \lambda^2\}
of the positive elliptic pseudo-differential operators on compact manifolds (with or without boundary).
6. A motivating problem
• The extension of the Lebeau-Robbiano/Jerison-Lebeau/Lebeau-Zuazua spectral inequality
\Vert \varkappa\Vert_{L^2(M)}\leq C_1e^{C_2 {\lambda}}\Vert \varkappa\Vert_{L^2(\omega)},\,\,\,\varkappa\in \textnormal{span}\{\rho_j:\lambda_j^\nu\leq \lambda^\nu\}.
(6)
to positive elliptic pseudo-differential operator E(x,D) of order \nu>0, implies the null-controllability for its corresponding diffusion model
\begin{cases}u_t(x,t)+ E(x,D) u(x,t)=g(x,t)\cdot 1_\omega (x) ,& (x,t)\in M\times (0,T), \\u(0,x)=u_0,\end{cases}
(7)
at any time T>0. Here \omega \subset M, \omega\neq \emptyset, is the controllability sensor. A natural question/motivating problem is to verify if this inequality remains valid for pseudo-differential operators.
7. Short overwiew about pseudo-differential operators
Pseudo-differential operators on \Bbb R^n [Kohn+Nirenberg 1965, Hörmander 1967]:
\widehat{f}(\xi) = \int_{\Bbb R^n} f(x)\ {\sf e}^{-2\pi \sf i} x\cdot\xi\ {\rm d}x, \quad Af(x) = \int_{\R^n} {\sf e}^{2\pi \sf i x\cdot\xi} \sigma_A(x, \xi) \widehat{f}(\xi) {\rm d}\xi,
\left| \partial_\xi^\alpha \partial_x^\beta \sigma_A(x,\xi) \right| \leq C_{\alpha\beta}\ \langle\xi\rangle^{m-\rho|\alpha|+\delta|\beta|}, \langle{\xi}\rangle=(1+|\xi|^2)^{1/2}, \xi\in\R^n.
\PsiDOs on the torus \Bbb T^n=\Bbb R^n/\Bbb Z^n: Fourier coefficients with \xi\in\mathbb{Z}^n,
\widehat{f}(\xi)= \int_{\Bbb T^n} f(x) {\sf e}^{-{\sf i}2\pi x\cdot\xi} \rm dx, \quad Af(x) = \sum_{\xi\in\Bbb Z^n} {\sf e}^\sf i 2\pi x\cdot\xi \sigma_A(x,{ \xi}) \widehat{f}(\xi),
\left| \triangle_\xi^\alpha \partial_x^\beta \sigma_A(x,\xi) \right| \leq C_{\alpha\beta}\ \langle\xi\rangle^{ m-\rho|\alpha|+\delta|\beta| }, \xi\in\Bbb Z^n.
[Agranovich 1990], [McLean 1991], [Turunen 2000],[Ruzhansky+Turunen, JFAA, 2010].
\PsiDOs on a compact Lie group G:
[Ruzhansky+Turunen, Birkhaüser book, 2010]
\widehat{f}(\xi) = \int_G f(x)\ \xi(x)^\ast\ {\rm d}x, \; Af(x) = \sum_{[\xi]\in\widehat G} d_{\xi} \ {\sf Tr}\left( \xi(x)\ { \sigma_A(x,\xi)}\ \widehat{f}(\xi) \right),
{ \|} { \triangle_\xi^\alpha} X^\beta \sigma_A(x,\xi) { \|_{op}} \leq C_{\alpha\beta}\ { \langle\xi\rangle}^{m-\rho|\alpha|+\delta|\beta|},\; {\xi\in \widehat G,} \ \langle{\xi}\rangle =e.v.,\ \Delta_\xi=\textnormal{diff.op.},\ \cdots.
8. Pseudo-differential operators on compact manifolds without boundary Kohn-Nirenberg+Hörmander
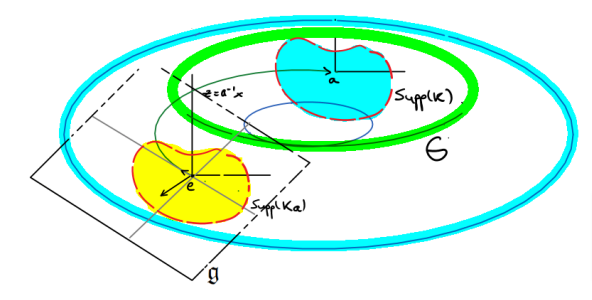
1. There is a well-known formulation of pseudo-differential operators on compact manifolds, (and so on compact Lie groups) by using symbols defined by charts.
2. If U\subset \R^n is open, the symbol a:U\times \R^n\rightarrow \mathbb{C}, belongs to the Hörmander class S^{ m}_{\rho},\delta({U\times \R^n}), 0\leqslant \rho,\delta\leqslant 1, if for every compact subset K\subset U, the symbol inequalities,
|\partial_{x}^\beta\partial_{\xi}^\alpha a(x,\xi)|\leqslant C_{\alpha,\beta,K}(1+|\xi|)^{ m} -\rho|\alpha|+\delta|\beta|,
hold true uniformly in x\in K and \xi\in \R^n.
3. Then, a continuous linear operator A:C^\infty_0(U) \rightarrow C^\infty(U)
is a pseudo-differential operator of order m, of (\rho,\delta)-type, if there exists
a function a\in S^m_{\rho,\delta}(U\times \R^n), satisfying
Af(x)=\int\limits_{\R^n}e^{2\pi i x\cdot \xi}a(x,\xi)(\mathscr{F}_{\R^n}{f})(\xi)d\xi,
for all f\in C^\infty_0(U), where
(\mathscr{F}_{\R^n}{f})(\xi):=\int\limits_Ue^{-i2\pi x\cdot \xi}f(x)dx,
is the Euclidean Fourier transform of f at \xi\in \R^n.
4. The class S^m_{\rho,\delta}(U\times \R^n) on the phase space U\times \R^n, is invariant under coordinate changes only if \rho\geqslant 1-\delta, while a symbolic calculus (closed for products, adjoints, parametrices, etc.) is only possible for \delta \lt \rho and \rho\geqslant 1-\delta. •
5. A:C^\infty_0(M)\rightarrow C^\infty(M) is a pseudo-differential operator of order m, of (\rho,\delta)-type, \rho\geqslant 1-\delta, if for every local coordinate patch \omega: M_{\omega}\subset M\rightarrow U\subset \R^n,
and for every \phi,\psi\in C^\infty_0(U), the operator
Tu:=\psi(\omega^{-1})^*A\omega^{*}(\phi u),\,\,u\in C^\infty(U), ^1
is a pseudo-differential operator with symbol in S^m_{\rho,\delta}(U\times \R^n). ^1 As usually, \omega^{*} and (\omega^{-1})^* are the pullbacks induced by the maps \omega and \omega^{-1}, respectively.}
9. Pseudo-differential operators on compact Lie groups (Ruzhansky-Turunen classes)
9.1. Basics on Representation theory
• Unitary representation \xi of a group G is \xi:G\to \mathcal{L}(\mathcal{H}_{\xi}), where \mathcal{H}_{\xi} is a Hilbert representation space, such that \xi(x)^*=\xi(x)^{-1} (unitary) and {\xi(xy)=\xi(x)\ \xi(y)} (preserves group structure).
• It is irreducible if \xi\not=\xi_{1}\oplus\xi_{2} for some unitary representations \xi_{1},\xi_{2}.
• If G is compact, it is enough to consider finite-dimensional \mathcal{H}_{\xi}, i.e. \xi:G\to {\mathbb C}^{d_{\xi}\times d_{\xi}} for d_{\xi}=\dim \mathcal{H}_{\xi} the dimension of \xi.
• Example: For \mathbb{T}^n, \xi_k(x)=e^{2\pi i x\cdot k}, k\in\mathbb{Z}^n. Then \xi_k:\mathbb{T}^n\to\mathbb{C}^{1\times 1}, d_{\xi_k}=1.
• The unitary dual \widehat{G} is defined (omitting equivalent classes) as
\widehat{G} = continuous irreducible unitary representations of G
• Fourier coefficient \widehat{f}(\xi) of f \in L^{1}(G) at \xi \in \widehat{G} is
\widehat{f}(\xi) = \int_G f(x)\ \xi(x)^*\ {\rm d}x.
Note that \widehat{f}(\xi)\in\mathcal{L}(\mathcal{H}_{\xi}) is now an operator; a matrix if G is compact.
• We define the weight \langle{\xi}\rangle to measure the growth of the Fourier coefficients. This is essential if talking about function spaces and about the symbol classes associated to the unique bi-invariant Riemannian structure on G (Laplacian).
For each \xi\in\widehat{G}, we have for the Laplacian:
-{\mathcal{L}}_{G} \xi=\lambda_\xi^2 \xi
In other words,
-{\mathcal{L}}_G \xi_{ij}(x)=\lambda_{\xi}^{2}\xi_{ij}(x),\quad 1\leq i,j\leq d_\xi.
We define
\langle {\xi}\rangle :=(1+\lambda_{\xi}^2)^{1/2}
These are the eigenvalues of the first order elliptic operator (1-\mathcal{L}_{G})^{1/2}, and we note that \langle {\xi}\rangle has here multiplicity d_{\xi}^{2}.
9.2. Operators on compact Lie groups
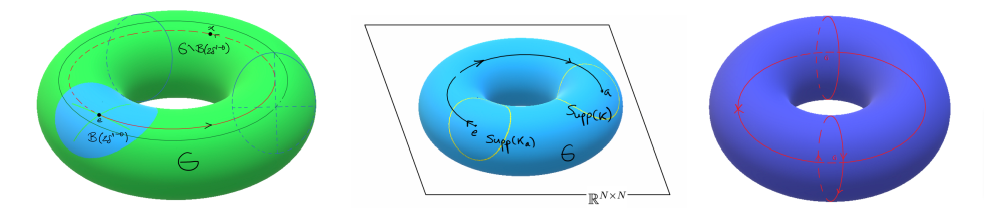
• If A:C^\infty(G)\to C^\infty(G) cont. \& linear, then we can define its symbol as
(x,\xi)\mapsto \sigma_A(x,\xi),\quad \sigma_A(x,\xi) := \xi(x)^* (A\xi)(x),
where (A\xi)_{ij}=A(\xi_{ij}) acts on components. This (full) symbol of A is matrix-valued: \sigma_A(x,\xi)\in\mathbb{C}^{d_\xi\times d_\xi}. Then we can show that
Af(x) = \sum_{\xi\in\widehat{G}} d_\xi {\rm Tr}\left( \xi(x) \sigma_A(x,\xi) \widehat{f}(\xi) \right).
This symbol is well-defined
on G\times\widehat{G} (non-commutative phase space).
There are many familiar features, e.g. if
Af(x)=\int_G K(x,y) f(y) dy=\int_G f(y) R_A(x,y^{-1}x)\ dy,
then \sigma_A(x,\xi)=\int_G R_A(x,y)\ \xi(y)^* dy (i.e. symbol is F.T. of the kernel).
We have (full) symbolic calculus for this quantization, and (!) with formulae resembling the familiar formulae on \R^n.
• As usual, \Psi^m_{\rho,\delta}(G) is the Hörmander class of pseudo-differential operators on G, i.e. such that their localisations have symbols in S^m_{\rho,\delta}(\R^n).
Let \langle{\xi}\rangle be the eigenvalue of (I-\mathcal{L}_G)^{1/2}, \mathcal{L}_G Laplacian, corresponding to \xi.
Now, we define the class of symbols \sigma_A\in S^m_{\rho,\delta}(G\times \widehat{G}) by
\| \triangle_\xi^\alpha X^{\beta}_{x} \sigma_A(x,\xi)\|_{op} \le C_{\alpha\beta} \langle\xi\rangle^{m-\rho|\alpha|+\delta|\beta|}
Independent of the choice of a strongly admissible collection for 1\leq \delta \lt \rho\leq 1.
• Ruzhansky-Turunen-Wirth Theorem: Let 0\leq \delta \lt \rho\leq 1, and \rho\geq 1-\delta. Then, A\in\Psi^m_{\rho,\delta}(G) if and only if \sigma_A\in S^m_{\rho,\delta}(G\times \widehat{G}).
10. Elliptic pseudo-differential operators on compact Lie groups and on general compact manifolds
• Let M be a closed manifold.
We say that an operator A\in \Psi^m_{\rho,\delta}(M) is elliptic of order m\in \R, if in any local coordinate system U, and for any compact subset K\subset{U}, its symbol satisfies the inequality
C_1 (1+|\theta|)^m\leq |a(x,\theta)|\leq C_2 (1+|\theta|)^m, |\theta|\geq R,
(8)
for some R>0, uniformly in x\in K, and \theta\in \R^n.
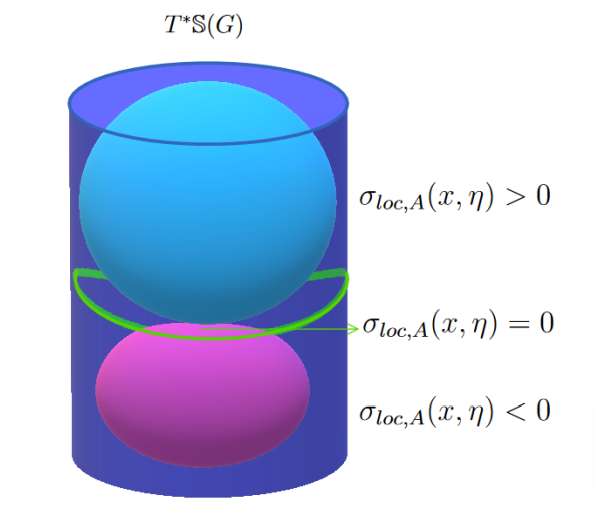
• We say that a matrix-valued symbol a:G\times \widehat{G}\rightarrow \cup_{\ell}\mathbb{C}^{\ell\times \ell}, is elliptic of order m\in \R if
– \exists R>0,\, a(x,[\theta])\in \textnormal{GL}(d_\theta,\mathbb{C}) is an invertible matrix for all \langle \theta\rangle\geq R.
– The following symbol inequality holds uniformly in x\in G, when \langle \theta\rangle\geq R:
\|( a(x,[\theta]))^{-1}\|_{\textnormal{op}}\leqslant C\langle\theta\rangle^{-m}.
11. Main results: Spectral inequalities for pseudo-differential operators and applications to control theory
• D. Cardona, 2022. Let \nu>0, and let 0\leq \delta \lt \rho\leq 1 be such that \rho\geq 1-\delta. Let E(x,D)\in \Psi^\nu_{\rho,\delta}(M) be an elliptic positive pseudo-differential operator of order \nu>0. Let (x,\xi)\in T^*M, and assume that for any \xi\neq 0, E(x,\xi)>0 is strictly positive. Then, for any non-empty open subset \omega\subset M, we have
\Vert \varkappa\Vert_{L^2(M)}\leq C_1e^{C_2 {\lambda}}\Vert \varkappa\Vert_{L^2(\omega)},\,\,\,\varkappa\in \textnormal{span}\{\rho_j:\lambda_j\leq \lambda\}.
(9)
• D. Cardona, 2022. For any R>0 let B(x,R) be a ball defined by the geodesic distance, of radius R>0 and centred at x. Then,
\sup_{B(x,2R)}|\varkappa|\leq e^{C_1' {\lambda}+C_2'} \sup_{B(x,R)}|\varkappa|,\,\,\,\varkappa\in \textnormal{span}\{\rho_j:\lambda_j\leq \lambda\},
(10)
with C_1'=C_{1}'(R) and C_2'=C_2'(R) are dependent only on the radius R>0 but not on \varkappa.
• D. Cardona, 2022. Let \nu>0, and let 0\leq \delta \lt \rho\leq 1 be such that \rho\geq 1-\delta. Let E(x,D)\in \Psi^\nu_{\rho,\delta}(M) be a positive elliptic pseudo-differential operator of order \nu>0. Let (x,\xi)\in T^*M, and assume that for any \xi\neq 0, E(x,\xi)>0 is strictly positive. Then,
for any \alpha>1/\nu, the fractional diffusion problem
\begin{cases}u_t(x,t)+ E(x,D)^\alpha u(x,t)=g(x,t)\cdot 1_\omega (x) ,& (x,t)\in M\times (0,T), \\u(0,x)=u_0,\end{cases}
(11)
is null-controllable at any time T>0, for any non-empty open subset \omega\subset M.
• D. Cardona, J. Delgado, M. Ruzhansky, 2022. Let 0\leq \delta \lt \rho\leq 1. Let A\in \Psi^m_{\rho,\delta}(G\times \widehat{G}) be a positive elliptic pseudo-differential operator of order m>0. Assume that \sigma_A(x,\xi)\geq 0 for all (x,[\xi])\in G\times \widehat{G}. Let (e_j,\lambda_j^m), \lambda_j\geq 0, be the corresponding spectral data of A, determined by the eigenvalue problem Ae_j=\lambda_j^me_j with the eigenfunctions e_j being L^2-normalised. Then the following spectral estimates are valid:
– For any non-empty open subset \omega\subset G, we have
\Vert \varkappa\Vert_{L^2(G)}\leq C_1e^{C_2 {\lambda}}\Vert \varkappa\Vert_{L^2(\omega)},\,\,\,\varkappa\in \textnormal{span}\{e_j:\lambda_j\leq \lambda\},
(12)
with C_1=C_1(\omega) and C_2=C_2(\omega) depending on \omega, but not on \varkappa. – For any R>0 let B(x,R) be a ball defined by the geodesic distance, of radius R>0 and centred at x. Then,
\sup_{B(x,2R)}|\varkappa|\leq e^{C_1' {\lambda}+C_2'} \sup_{B(x,R)}|\varkappa|,\,\,\,\varkappa\in \textnormal{span}\{e_j:\lambda_j\leq \lambda\},
(13)
with C_1'=C_{1}'(R) and C_2'=C_2'(R) depending only on the radius R>0 but not on \varkappa.
\end{itemize}
• D. Cardona, J. Delgado, M. Ruzhansky, 2022. Let A be a positive and elliptic pseudo-differential operator of order m > 0 in the Hörmander class \Psi^ m _{\rho,\delta}(G\times \widehat{G}) and let u_0\in L^2(G) be an initial datum. Asuma that \sigma_A(x,[\xi])\geq 0 for all (x,[\xi])\in G\times \widehat{G}.
Then, for any \alpha>1/ m , the fractional diffusion model
\begin{cases}u_t(x,t)+ A^\alpha u(x,t)=g(x,t)\cdot 1_\omega (x) ,& (x,t)\in G\times (0,T), \\u(0,x)=u_0,\end{cases}
(14)
is null-controllable at any time T>0, that is, there exists an input function g=g(x,t)\in L^2(G) such that for any x\in G, u(x,T)=0.
References
[1] D. Cardona, Spectral inequalities for elliptic pseudo-differential operators on closed manifolds, arXiv:2209.10690.
[2] D. Cardona, J. Delgado, M. Ruzhansky. Estimates for sums of eigenfunctions of elliptic pseudo-differential operators on compact Lie groups, arXiv:2209.12092.}
[3] H. Donnelly and C. Fefferman, Nodal sets of eigenfunctions on Riemannian manifolds, Invent. Math. 93, 161–183, (1988).
[4] V. Fischer, M. Ruzhansky. Quantization on nilpotent Lie groups, Progress in Mathematics, Vol. 314, Birkhauser, 2016. xiii+557pp.
[5] D. Jerison, G. Lebeau. Nodal sets of sums of eigenfunctions. Harmonic analysis and partial differential equations (Chicago, IL, 1996), Chicago Lectures in Math, 223–239, (1999).
[6] L, Hörmander. The Analysis of the linear partial differential operators} Vol. III. Springer-Verlag, (1985).
[7] G. Lebeau, L. Robbiano, Controle exact de l’equation de la chaleur, Comm. Partial Diff. Equations., 20, 335–356, (1995).
[8] G. Lebeau, E. Zuazua. Null-Controllability of a System of Linear Thermoelasticity. Arch. Rational Mech. Anal. 141(4), 297–329, (1998).
[9] L. Miller. On the controllability of anomalous diffusions generated by the fractional Laplacian. Math. Control Signals Systems 18(3), 260–271, (2006).
[10] L. Miller. On the cost of fast controls for thermoelastic plates, Asymptot. Anal. 51, 93–100, (2007).
[11] M. Ruzhansky, V. Turunen. Pseudo-differential Operators and Symmetries: Background Analysis and Advanced Topics, Birkhauser, Basel, 2010. 724pp.


