1 Introduction
In the post IpOpt and AMPL use to solve time optimal control problems, we explain how to use IpOpt and AMPL in order to solve control problems with control constraints and possibly some state constraints.
In the present post, we are going to present a numerical development in order to find the minimal controllability time for the discretized heat equation with unilateral (non-negative) control constraint. More precisely, we consider the controllability of a discretized version of the 1D heat equation under nonnegative Dirichlet control constraint. The infinite dimensional system, we consider is
\[
\dot{\psi}(t,x) & = \partial_x^2 \psi(t,x) \qquad \qquad && \qquad \qquad ( t>0,\, x\in(0,1)),\\
\]
\[
\partial_x\psi(t,0) & = 0 \qquad \qquad && \qquad \qquad (t>0),\\
\]
\[
\psi(t,1) & = u(t) \qquad \qquad && \qquad \qquad (t>0),\\
\]
\[
\psi(0,x) & = \psi^0(x) \qquad \qquad && \qquad \qquad (x\in(0,1)),\\
\]
where $\psi$ is the state to control $\psi^0$ the initial state and $u$ the Dirichlet control.
The continuous version of this problem has been analysed in [2] and it has been shown that for every initial state $\psi^0\in L^2(0,1)$ and every positive constant target $\psi^1$, the controllability of this system under the control constraint
\begin{equation}\label{eq:ContConst}
u(t)\geqslant0\qquad (t\geqslant 0),
\end{equation}
requires a positive waiting time as soon as the target state $\psi^1$ is different from the initial state $\psi^0$.
In this post, we consider a spatially discretized version with has the form
\begin{equation}\label{eq:SysGen}
\dot{y}(t)=Ay(t)+B u(t)\qquad (t>0),
\end{equation}
where the matrices $A$ and $B$ are
\begin{equation}\label{eq:ABheat}
A=(n+1)^2\begin{pmatrix}
-2 & 2 & 0 & \hdots& \hdots& 0\\
1 & -2 & 1 & 0 & \hdots& 0\\
0 & \ddots& \ddots& \ddots& \ddots& \vdots\\
\vdots& \ddots& \ddots& \ddots& \ddots& 0\\
\vdots& & \ddots& \ddots& \ddots& 1\\
0 & \hdots& \hdots& 0 & 1 & -2
\end{pmatrix}\in M_{n}(\mathbb{R})\quad\text{and}\quad B=(n+1)^2\begin{pmatrix}
0\\
\vdots\\
\vdots\\
\vdots\\
0\\
1
\end{pmatrix}\in M_{n,1}(\mathbb{R}).
\end{equation}
where $n+1>2$ is the number of discretization points and $[y]_i(t)$ (the $i^\text{th}$ component of $y(t)\in\mathbb{R}^n$) stands for $\psi(t,(i-1)/n)$.
To obtain the above finite dimensional system, we have used centred finite differences.
The aim is then to minimize the time $T$ such that there exist a control $u:[0,T]\to\mathbb{R}_+$ steering the solution of (\ref{eq:SysGen}) from $y^0\in\mathbb{R}^n$ to $y^1\in\mathbb{R}^n$ in time $T$. For the sake of simplicity, we assume that $y^0$ and $y^1$ are constant vectors of $\mathbb{R}^n$, that is to say that
\begin{equation}\label{eq:y0y1}
y^0=u^0\begin{pmatrix}1\\\vdots\\1\end{pmatrix}\in\mathbb{R}^n\quad\text{ and }\quad y^1=u^1\begin{pmatrix}1\\\vdots\\1\end{pmatrix}\in\mathbb{R}^n,
\end{equation}
for some $u^0\in\mathbb{R}$ and $u^1\in\mathbb{R}$ Since the control $u$ shall satisfy the constraint (\ref{eq:ContConst}), it is easy to see, using a discrete version of the comparison principle, that in order to have the existence of a solution, then we need $u^1>0$.
Note that, using again the comparison principle, we can also show that if $u^0\geqslant 0$ then, whatever the control $u\geqslant 0$ is, the solution of (\ref{eq:SysGen}) always satisfies $y(t)\geqslant 0$.
To conclude, the optimization problem we aim to solve is
\begin{equation}\label{eq:optim0}
\begin{array}{cl}
\inf & T\\
\vline & \begin{array}{l}
T\geqslant 0,\\
y(T;u;y^0)=y^1,\\
u\in L^\infty(0,T),\quad u(t)\geqslant 0\quad (t\in[0,T]\text{ a.e.}),
\end{array}
\end{array}
\end{equation}
where $y^0$ and $y^1$ are given by (\ref{eq:y0y1}) for some $u^0\in\mathbb{R}$ and $u^1\in\mathbb{R}_+^*$, and where $y(t;u;y^0)$ stands for the solution of (\ref{eq:SysGen}) at time $t$, with control $u$ and initial condition $y^0$.
In this post, in order to find numerically the minimal controllability time and a time-optimal control, we are going to use the abstract result presented in the next paragraph. Another way could be to introduce, in addition to the control constraint $u(t)\geqslant 0$, the additional control constraint $u(t)\leqslant M$, and let $M$ increase to $+\infty$. Such an approach has been introduced in the previous post IpOpt and AMPL use to solve time optimal control problems.
2 Abstract result
It is shown in [1] that at the minimal time $\underline{T}(y^0,y^1)$, defined by (\ref{eq:optim0}), there exists a non-negative control $u$ in the class of Radon measure.
Furthermore, it is proved in this article that at the minimal controllability time, there exists one and only one non-negative Radon measure and this time optimal control is a convex sum of at most $\lfloor (n+1)/2 \rfloor$ Dirac masses.
In other words, the non-negative time optimal control takes the form:
$$u=\sum_{k=1}^N\alpha_k\delta_{t_k},$$
with $N=\lfloor (n+1)/2 \rfloor$, $0\leqslant \alpha_k$ and $0\leqslant t_1\leqslant\dots\leqslant t_N\leqslant T$.
For a control of this form, the solution of (\ref{eq:SysGen}) at time $T$, with initial condition $y^0$, is:
$$y(T)=e^{TA}y^0+\sum_{k=1}^N \alpha_i e^{(T-t_k)A}B.$$
Consequently, the minimal time $\underline{T}(y^0,y^1)$ given by (\ref{eq:optim0}) is a minimizer of:
\begin{equation}\label{eq:optim1}
\begin{array}{cl}
\inf & T\\[1mm]
\vline & \begin{array}{l}
0\leqslant t_1\leqslant\dots\leqslant t_N\leqslant T,\\[2mm]
\alpha_1,\dots,\alpha_N\geqslant 0,\\[1mm]
\displaystyle{y^1-e^{TA}y^0=\sum_{k=1}^N \alpha_k e^{(T-t_k)A}B}.
\end{array}
\end{array}
\end{equation}
3 Numerical implementation
The optimization problem (\ref{eq:optim1}) is not easy to solve directly, mainly because of the presence of a matrix exponential.
Thus, instead we will solve the discretized heat equation on each time interval $(t_k,t_{k+1})$, with $t_0=0$ and $t_{N+1}=T$.
Let us then set $\tau_k=t_{k+1}-t_k$ for every $k\in\{0,\dots,N\}$.
We have $T=\sum_{k=0}^N\tau_k$ and the optimization problem (\ref{eq:optim1}) also writes
\[
\begin{array}{cl}
\inf & \displaystyle{\sum_{k=0}^N\tau_k}\\[1mm]
\vline & \begin{array}{l}
0\leqslant \tau_k\qquad (k\in\{0,\dots,N\}),\\
0\leqslant \alpha_k\qquad (k\in\{1,\dots,N\}),\\
y_0(0)=y^0,\\
y_{k+1}(0)=y_k(\tau_k)+\alpha_{k+1}B\qquad(k\in\{0,\dots,N-1\}),\\
y_{N}(\tau_N)=y^1,\\
\text{~\qquad where $y_k(t)=e^{tA}y_k(0)$, i.e.~$y_k$ is solution of (2) with null control.}
\end{array}
\end{array}
\]
In the above constraints, $y_k(\tau)=y(\tau+t_k)$ for every $\tau\in(0,\tau_k)$, where $y$ is the solution of (\ref{eq:SysGen}), with control $u=\sum_{k=1}^N\alpha_k\delta_{t_k}$ and initial condition $y(0)=y^0$. Notice that since $\alpha_k$ is only constrained to be non-negative, and since the vector $B$ (given by (\ref{eq:ABheat})) is of the form $(0,\dots,0,b_n)^\top$, with $b_n\geqslant 0$, the constraint $y_{k+1}(0)=y_k(\tau_k)+\alpha_{k+1}B$ can be expressed as
\begin{equation*}
[y_{k+1}]_n(0)\geqslant [y_k]_n(\tau_k)
\qquad\text{and}\qquad
[y_{k+1}]_i(0)=[y_k]_i(\tau_k)\qquad (i\in\{1,\dots,n-1\}).
\end{equation*}
Consequently, the parameters $\alpha_1,\dots,\alpha_N$ can be forgotten.
In order to numerically compute $y_k(t)=e^{tA}y_k(0)$ for $t\in[0,\tau_k]$, we are going to use the Crank-Nicholson method.
More precisely, given $N_t\in\mathbb{N}^*$, we approximate $y_k(j\tau_k/N_t)$ by $y_k^j$, with $y_k^j$ solution of
$$y_k^0=y_k(0),\qquad \left( \mathrm{I}_n-\frac{\tau_k}{2N_t}A \right)y_k^{j+1}=\left( \mathrm{I}_n+\frac{\tau_k}{2N_t}A \right)y_k^j\qquad (j\in\{0,\dots,N_t-1\}).$$
All in all, the fully discretized optimization problem, is
\begin{equation}\label{eq:optD1}
\min\ \sum_{k=0}^N \tau_k,
\end{equation}
subject to the constraints
\begin{align}
\label{eq:optD2}
& 0\leqslant \tau_k\qquad (k\in\{0,\dots,N\}),\\
\end{align}
\begin{align}
\label{eq:optD3}
& [y_0^0]_i=u^0\qquad (i\in\{1,\dots,n\}),\\
\end{align}
\begin{align}
\label{eq:optD4}
& [y_{k+1}^0]_j=[y_k^{N_t}]_j\qquad(k\in\{0,\dots,N-1\},\ j\in\{1,\dots,n\}),\\
\end{align}
\begin{align}
\label{eq:optD5}
& [y_{k+1}^0]_n\geqslant [y_k^{N_t}]_n\qquad(k\in\{0,\dots,N-1\}),\\
\end{align}
\begin{align}
\label{eq:optD6}
& \max_{i\in\{1,\dots,n\}}\left|[y_{N}^{N_t}]_i-u^1\right|\leqslant \varepsilon,\\
\end{align}
\begin{align}
\label{eq:optD7}
& \left( \mathrm{I}_n-\frac{\tau_k}{2N_t}A \right)y_k^{j+1}=\left( \mathrm{I}_n+\frac{\tau_k}{2N_t}A \right)y_k^j\qquad (k\in\{0,\dots,N\},\ j\in\{0,\dots,N_t-1\}).
\end{align}
Note that instead of imposing $[y_{N}^{N_t}]_i=u^1$, we chose to relax this condition in the constraint (\ref{eq:optD6}).
This choice has been a maid since we do not expect that the numerical solution exactly reaches the target $y^1$. In practice, we will take, $\varepsilon=1/(n\, N_t)$.
In term of AMPL language, the above constrained optimization problem is
# define parameters param n = 20; # number of spatial discretization points param Nt = 400; # number of time discretization points param N = floor((n+1)/2); # maximal number of control impulses param eps= 1/(n*Nt); # relaxation parameter $\varepsilon}$ in (\ref{eq:optD6}) param u0 = 1; # parameters $u^0\text{ and }u^1}$, see (\ref{eq:y0y1}) param u1 = 5; # define variables var y {k in 0..N, j in 0..Nt, i in 1..n}; # unknowns $[y_k^j]_i$ var tau {k in 0..N} >=0; # unknown impulse times $\tau_k}$ subject to (\ref{eq:optD2}) # objective function, see (\ref{eq:optD1}) minimize T: sum {k in 0..N} tau[k]; # define the constraints # constraint (\ref{eq:optD7}) for interior points subject to y_dyn {k in 0..N, j in 1..Nt, i in 2..n-1}: y[k,j,i]-y[k,j-1,i] = (n+1)^2*(y[k,j,i-1]-2*y[k,j,i]+y[k,j,i+1] +y[k,j-1,i-1]-2*y[k,j-1,i]+y[k,j-1,i+1])/2*tau[k]/Nt; # constraint (\ref{eq:optD7}) for i=n subject to y_dyn_Dirichlet {k in 0..N, j in 1..Nt}: y[k,j,n]-y[k,j-1,n] = (n+1)^2*(y[k,j,n-1]-2*y[k,j,n]+y[k,j-1,n-1]-2*y[k,j-1,n])/2*tau[k]/Nt; # constraint (\ref{eq:optD7}) for i=1 subject to y_dyn_Neuman {k in 0..N, j in 1..Nt}: y[k,j,1]-y[k,j-1,1] = (n+1)^2*(y[k,j,2]-y[k,j,1]+y[k,j-1,2]-y[k,j-1,1])/2*tau[k]/Nt; # initial condition, constraint (\ref{eq:optD3}) subject to y_init {i in 1..n}: y[0,0,i] = u0; # terminal condition, constraint (\ref{eq:optD6}) subject to y_end1 {i in 1..n}: y[N,Nt,i] >= u1-eps; subject to y_end2 {i in 1..n}: y[N,Nt,i] <= u1+eps; # constraint (\ref{eq:optD4}) subject to continuity {k in 0..N-1, i in 1..n-1}: y[k+1,0,i]=y[k,Nt,i]; # constraint (\ref{eq:optD5}) subject to jump {k in 0..N-1}: y[k+1,0,n]>=y[k,Nt,n]; # solve the problem with IpOpt option solver ipopt; option ipopt_options "max_iter=100000 linear_solver=mumps halt_on_ampl_error yes"; solve; # display parameters and solution printf: "u0 = %24.16e\n", u0; printf: "u1 = %24.16e\n", u1; printf: "T = %24.16e\n", T; printf: "n = %d\n", n; printf: "Nt = %d\n", Nt; printf: "N = %d\n", N; printf: "Data\n"; printf: "t_k ="; printf {k in 0..N}: " %24.16e\t", tau[k]; printf: "\n"; printf: "y =\n"; for {k in 0..N} { printf "k = %d\n", k; printf {j in 0..Nt, i in 1..n}: " %24.16e\n", y[k,j,i]; } end; # quit AMPL
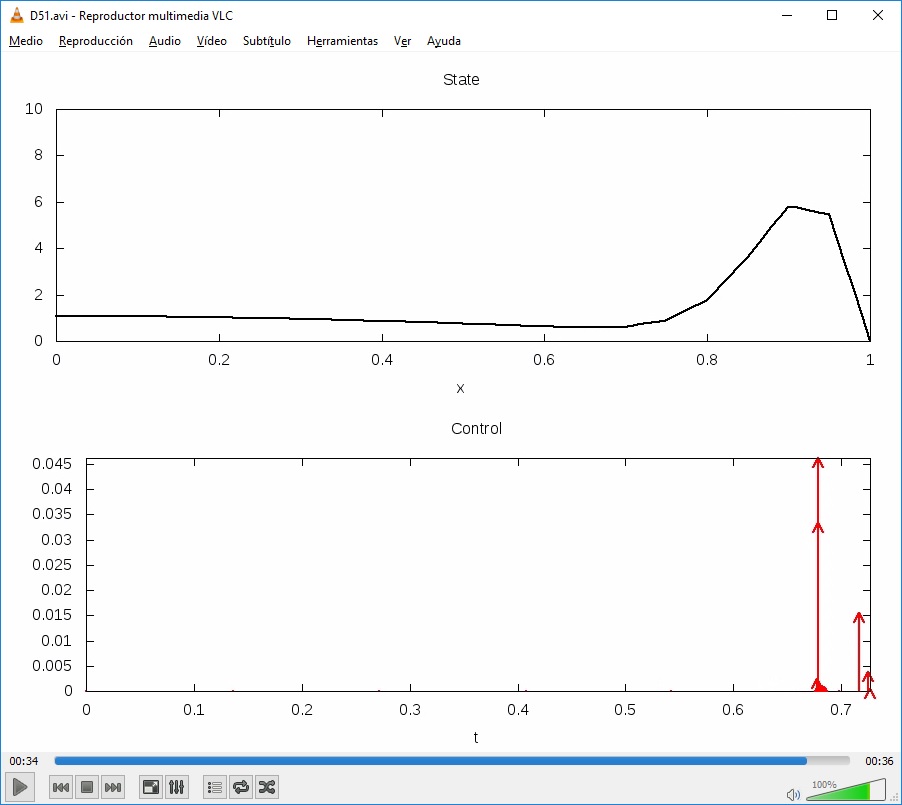
In the following simulations, we take n=20 and N_t=400. By post-treatment of the results (see the Scilab file in the post IpOpt and AMPL use to solve time optimal control problems for an example), we obtain the following results:
- for $u^0=1$ and $u^1=5$: The minimal time obtained is $\mathtt{0.1689856}$.
- for $u^0=5$ and $u^1=1$: The minimal time obtained is $\mathtt{0.7267605}$.
In the above videos, red arrows correspond to Dirac masses in the control.
References
[1] J. Lohéac, E. Trélat, and E. Zuazua. Control of the semi-discrete 1D heat equation under nonnegative control constraint. In preparation.
[2] J. Lohéac, E. Trélat, and E. Zuazua. Minimal controllability time for the heat equation under state constraints. Mathematical Models and Methods in Applied Sciences, Volume 27, Issue 09, August 2017