The turnpike property
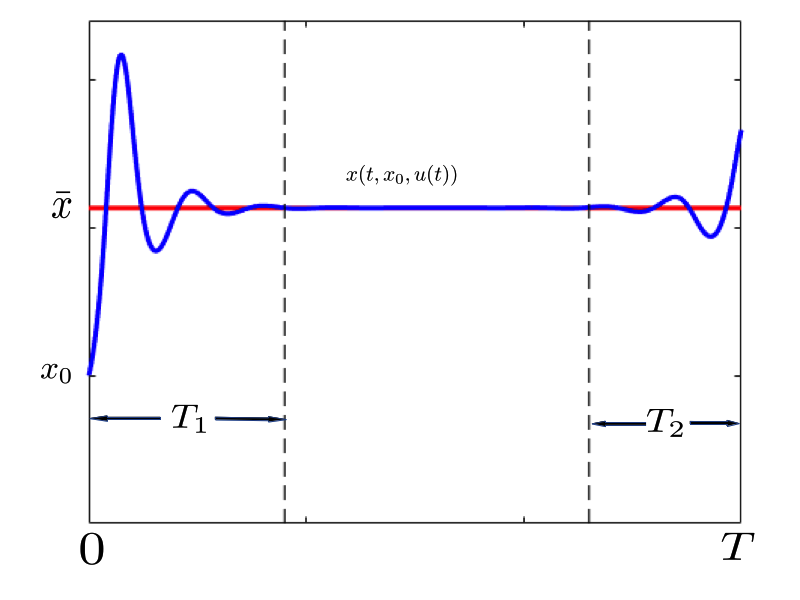
The turnpike property establishes that, when a general optimal control problem is settled in large time, for most of the time the optimal control and trajectories remain exponentially close to the optimal control and state of the corresponding steady-state or static optimal control problem.
The origin of the term Turnpike is in the interpretation that Samuelson did of this phenomenon in [1] : suppose we want to travel from city A to city B by car, the best way to do it, the optimal way, is to take the highway (namely, the turnpike) as near as we can from city A, and leave it when we are close to B. So, except nearby A and B, we are expected to be on the highway: in other words, the turnpike of the problem.
The turnpike property is very useful, since it gives us an idea of the nature of the optimal solution of a problem, without having to solve it analytically. In practice, the turnpike property allows performing a significant improvement of the numerical methods used to solve optimal control problems.
The Turnpike property in the Linear Case
Consider the finite-dimensional dynamical system
\begin{equation}
\left\lbrace
\begin{array}{ccc}
\label{linearproblem}
& x_t + Ax = Bu\\
& x(0)=x_0 \in \mathbb{R}^{N}
%\nonumber
\end{array}
\right.
\end{equation}
where $A \in M(N,N)$, $B\in M(N,M)$, with control $u \in L^2 (0,T;\mathbb{R}^{N})$. Given a matrix $C \in M(N,N)$, and some $x^* \in \mathbb{R}^{N}$, consider the optimal control problem
\begin{equation}
\min_{u} J^T (u) = \frac{1}{2} \int_0^T \left( |u(t)|^2 + |C(x(t)-x^*)|^2 \right)dt.
\end{equation}
There exists a unique optimal control $u(t)$ in $ L^2 (0,T;\mathbb{R}^{M})$, characterized by the optimality condition
\begin{equation} u = - B^*p, \,\,\,\,\,\, \left\lbrace \begin{array}{ccc} \label{linearproblem} & -p_t + A^* p = C^*C(x-x^*)\\ & p(T)=0 \in \mathbb{R}^{N} %\nonumber \end{array} \right. \end{equation}Let formulate the same problem for the steady-state model
\begin{equation} Ax=Bu. \end{equation}Then, there exists a unique minimum $\bar{u}$, and a unique optimal state $\bar{x}$, of the stationary optimal control problem
\begin{equation} %\nonumber \left\lbrace \begin{array}{clc} & \min_{u} J_s (u) = \frac{1}{2} \left( |u|^2 + |C(x -x^*)|^2 \right). \ \\ & subject \,\,\, to\,\,\, Ax=Bu \end{array} \right. \end{equation}Let assume that:
- The pair $(A,B)$ is controllable.
- The pair $(A,C)$ is observable.
Then, we have the following result (proved in [2])
Theorem: there exist positive constants $\lambda$ and $K$, independent on $T$, such that $ \forall t \in [0,T]$
$$
|u(t) -\bar{u}| + |x(t) – \bar{x}| \leq K \left( e^{-\lambda t} + e{-\lambda (T-t)} \right) .
$$
Some results and extensions on the turnpike property
- Turnpike theorems were derived in the 60’s for discrete-time optimal control problems arising in econometry [3] and references therein).
- See [4], [5] and the references therein for an extensive overview of turnpike results
- In [6] they proved a turnpike theorem for nonlinear finite–dimensional systems, involving the state, the control and also the adjoint. Besides that, they explain how the turnpike can be used to improve certain numerical methods.
- A turnpike theorem for the 1-D wave equation with a homogeneous Dirichlet boundary condition at one side, and a Neumann boundary control action at the other can be found in [7].
- A turnpike theorem for the two–dimensional Navier-Stokes Equation is proved in [8], for both time depending and non-depending control.
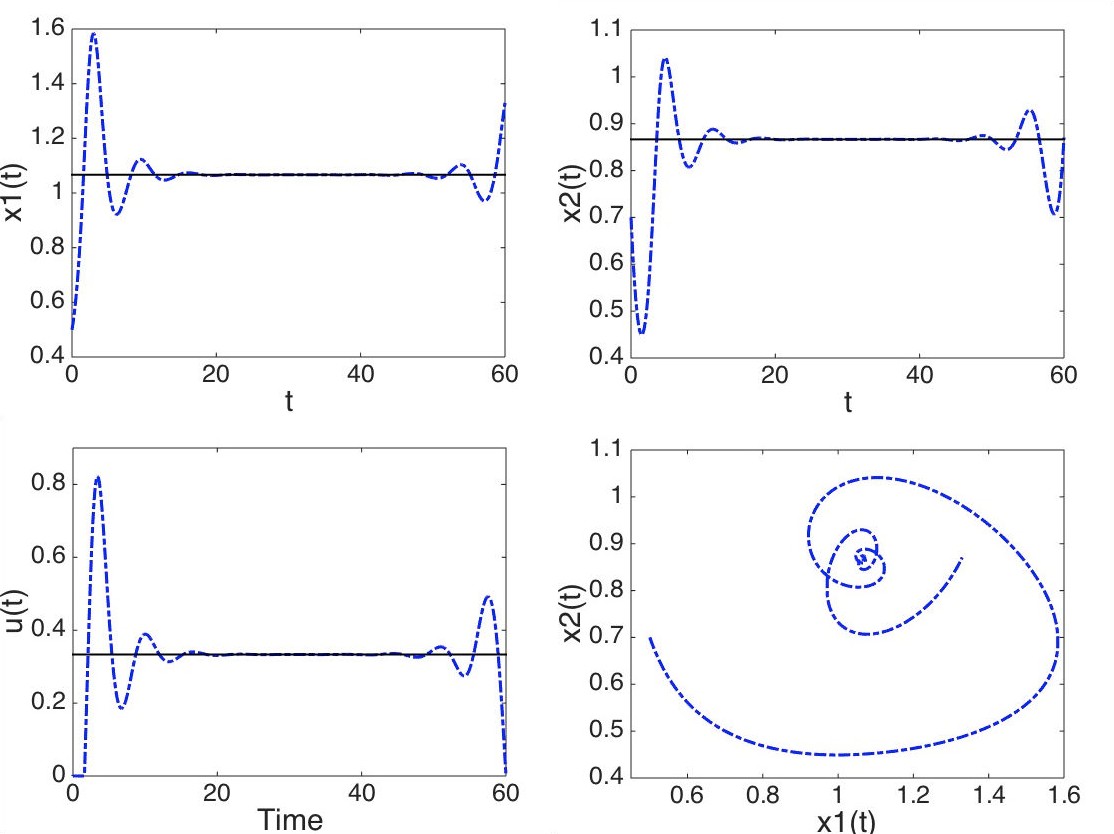
- An application of the turnpike property to the Lotka-Volterra model can be found in [9]. The property is used to improve the single shooting method to solve the problem.
Perspectives
- The study of the periodic turnpike property for optimal control problems in Hilbert spaces (in progress, E.Trélat, C. Zhang and E. Zuazua)
- Clarify the turnpike property for nonlinear PDE without smallness conditions on the target.
- The turnpike property on multi-D wave equations.
- Prove a turnpike theorem for a constrained control for linear and nonlinear finite–dimensional optimal control problems.
- Develope the turnpike computational code to solve a wide range of problems as it has been done in [9] for the Lotka-Volterra model.
References
[1] Robert Dorfman, Paul Anthony Samuelson, and Robert M Solow Linear programming and economic analysis. Courier Corporation, 1958.
[2] Alessio Porretta and Enrique Zuazua. Long time versus steady state optimal control. SIAM Journal on Control and Optimization, 51(6):4242–4273, 2013.
[3] Lionel W McKenzie. Turnpike theory. Econometrica: Journal of the Econometric Society, pages 841–865, 1976.
[4] Dean Carlson, Alain B Haurie, and Arie Leizarowitz. Infinite horizon optimal control: deterministic and stochastic systems. Springer Science & Business Media, 2012.
[5] Alexander Zaslavski. Turnpike properties in the calculus of variations and optimal control, volume 80. Springer Science & Business Media, 2006.
[6] Emmanuel Trélat and Enrique Zuazua. The turnpike property in finite-dimensional nonlinear optimal control Journal of Differential Equations, 258(1):81–114, 2015.
[7] Martin Gugat, Emmanuel Trélat, and Enrique Zuazua. Optimal Neumann control for the 1D wave equation: finite horizon, infinite horizon, boundary tracking terms and the turnpike property Systems & Control Letters, 90:61–70, 2016.
[8] S Zamorano. The turnpike property for two-dimensional navier-stokes equations. arXiv preprint arXiv:1601.04984, 2016.
[9] Aitziber Ibañez. Optimal control of the Lotka–Volterra system: turnpike property and numerical simulations. Journal of Biological Dynamics, 11(1):25–41, 2017.

