Yesterday November 10th, our Postdoctoral researcher Jon Asier Bárcena Petisco gave a talk in the “Control in Times of Crisis” Seminar about: “Averaged dynamics and control for heat equations with random diffusion”
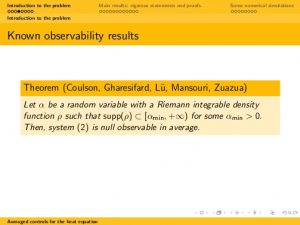
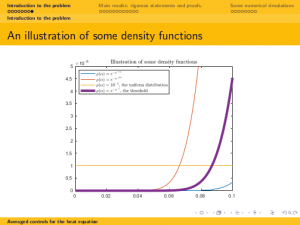
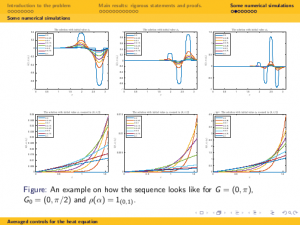
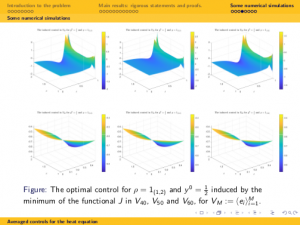
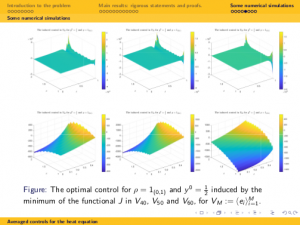
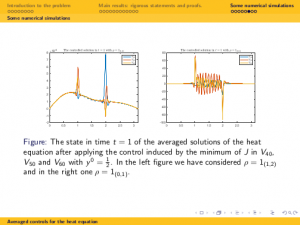
Abstract. In this talk we deal with the averaged dynamics for heat equations in the degenerate case where the diffusivity coefficient, assumed to be constant, is allowed to take the null value. First we prove that the averaged dynamics is analytic. This allows to show that, most often, the averaged dynamics enjoys the property of unique continuation and is approximately controllable. We then determine if the averaged dynamics is actually null controllable or not depending on how the density of averaging behaves when the diffusivity vanishes. In the critical density threshold the dynamics of the average is similar to the 1/2-fractional Laplacian, which is well-known to be critical in the context of the controllability of fractional diffusion processes. Null controllability then fails (resp. holds) when the density weights more (resp. less) in the null diffusivity regime than in this critical regime.
This talk is based on joint work with our Head Enrique Zuazua.
You can watch this talk cortesy by ControlPDE Youtube’s Channel:
See the slides of this talk: