I. Mazari, D. Ruiz-Balet. A fragmentation phenomenon for a non-energetic optimal control problem: optimisation of the total population size in logistic diffusive models (2020)
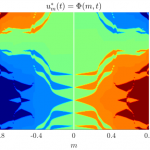
Abstract. Following the recent works [9, 17, 30, 31, 37], we investigate the problem of optimising the total population size for logistic diffusive models with respect to resources distributions. Using the spatially heterogeneous Fisher-KPP equation, we obtain a surprising fragmentation phenomenon: depending on the scale of diffusivity (i.e the dispersal rate), it is better to either concentrate or fragment resources. Our main result is that, the smaller the dispersal rate of the species in the domain, the more optimal resources distributions tend to oscillate. This is in sharp contrast with other criteria in population dynamics, such as the classical problem of optimising the survival ability of a species, where concentrating resources is always favourable, regardless of the diffusivity. Our study is completed by numerous numerical simulations that confirm our results.