Next Wednesday July 27, 2022 our visiting scientists at DeustoCCM, Jean-Daniel Djida and Weiwei Hu, will talk in a double session as part of the CCM – Chair of Computational Mathematics seminars, on:

• 10:30H “Optimal control of mixed local-nonlocal parabolic PDE”
By Jean-Daniel Djida

Slides

Abstract. Optimal Control Theory is one of the key subjects as it plays a crucial role in several areas, both in mathematics and outside such as in the modern theory of Machine Learning. In this talk, we will present recent developments on the widely open question of finding an appropriate notion of optimal control for mixed local-nonlocal PDEs. In order not to hide the flow of ideas by unnecessary technical complications, we shall focus on an operator that deals with the superposition of a Laplacian and a fractional Laplacian on a bounded domain. Operators of this type arise naturally from the coexistence of two stochastic processes with different scales.

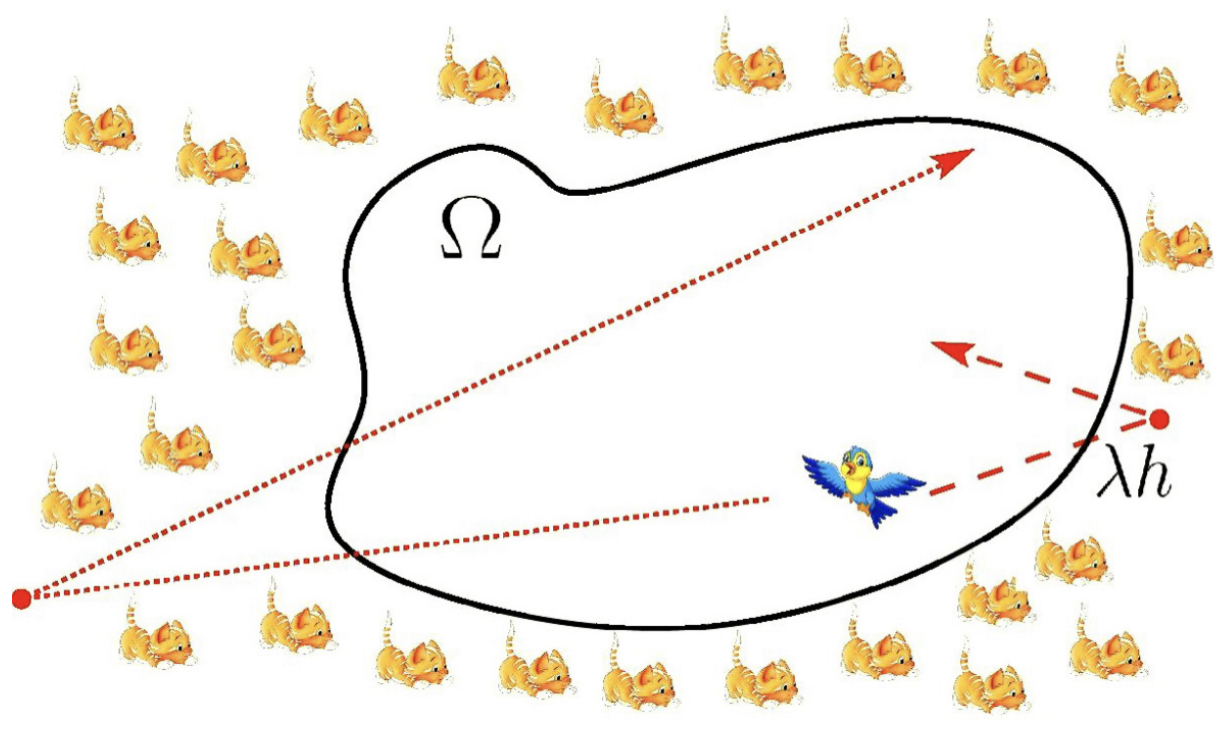
Image credits: Serena Dipierro and Enrico Valdinoci. Description of an ecological niche for a mixed local/nonlocal dispersal: an evolution equation and a new Neumann condition arising from the superposition of Brownian and Levy processes. Phys. A, 575:Paper No. 126052, 20, 2021.

• 11:00H “DeustoCCMSeminar: Nonlinear Feedback Control Design for Fluid Mixing”
By Weiwei Hu

Slides

Abstract. We discuss the problem of nonlinear feedback control design for fluid mixing via advection. The overall dynamics are governed by the transport and Stokes equations in an open bounded and connected domain. The feedback laws are constructed based on the ideas of instantaneous control as well as a direct approximation of the optimality system derived from an optimal open-loop control problem. It can be shown that under appropriate numerical discretization schemes, two approaches generate the same sub-optimal feedback law. On the other hand, different discretization schemes may result in feedback laws of different regularity, which determine different mixing results. The Sobolev norm of the dual space (H^{1}(\Omega))’ of H^{1}( \Omega) is used as the mix-norm to quantify mixing based on the known property of weak convergence. One of the major challenges is encountered in the analysis of the asymptotic behavior of the closed-loop systems, due to the absence of diffusion in the transport equation together with its nonlinear coupling with the flow equations. To address these issues, we first establish the decay properties of the velocity, which in turn help obtain the estimates on scalar mixing and its long-time behavior. Finally, mixed continuous Galerkin (CG) and discontinuous Galerkin (DG) methods are employed to discretize the closed-loop system. Numerical experiments are conducted to demonstrate our ideas and compare the effectiveness of different feedback laws.