B. Geshkovski, E. Zuazua, Optimal actuator design via Brunovsky's normal form (2022) IEEE Automatic Control, Vol. 26, No. 12, DOI: 10.1109/TAC.2022.3181222 Abstract: In this paper, by using the Brunovsky normal…
B. Geshkovski, E. Zuazua, Turnpike in Optimal Control PDES, ResNets and beyond (2022) Acta Numer., Vol. 31, pp. 135-263. doi:10.1017/S0962492922000046 Abstract: The turnpike property in contemporary macroeconomics asserts that if…
J.A. Bárcena-Petisco, M. Cavalcante, G.M. Coclite, N. de Nitti, Enrique Zuazua. Control of Hyperbolic and Parabolic Equations on Networks and Singular limits (2021) Abstract. We study the controllability properties of the…
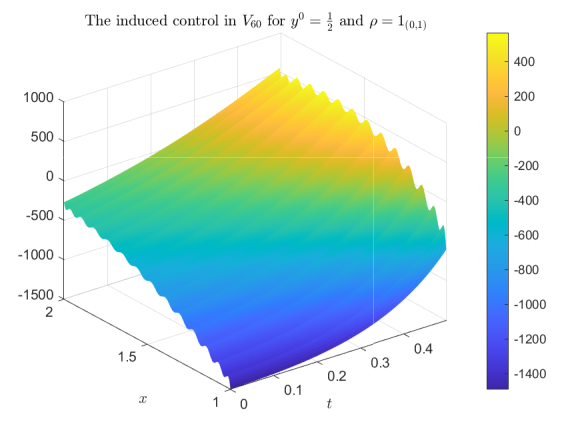
Today December 3rd our Postdoctoral member Jon Asier Bárcena Petisco talked about "Some recent results about the controllability of the heat equation" at the event 3rd. BYMAT - Bringing Young Mathematicians…
Next Thursday December 3rd our Postdoctoral member Jon Asier Bárcena Petisco is talking about "Some recent results about the controllability of the heat equation" at the event 3rd. BYMAT - Bringing…
Ruiz-Balet D., Zuazua E.. Control under constraints for multi-dimensional reaction-diffusion monostable and bistable equations. J. Math. Pures Appl, vol. 143, pp. 345-375 (2020) https://doi.org/10.1016/j.matpur.2020.08.006 Abstract. Dynamic phenomena in social and…