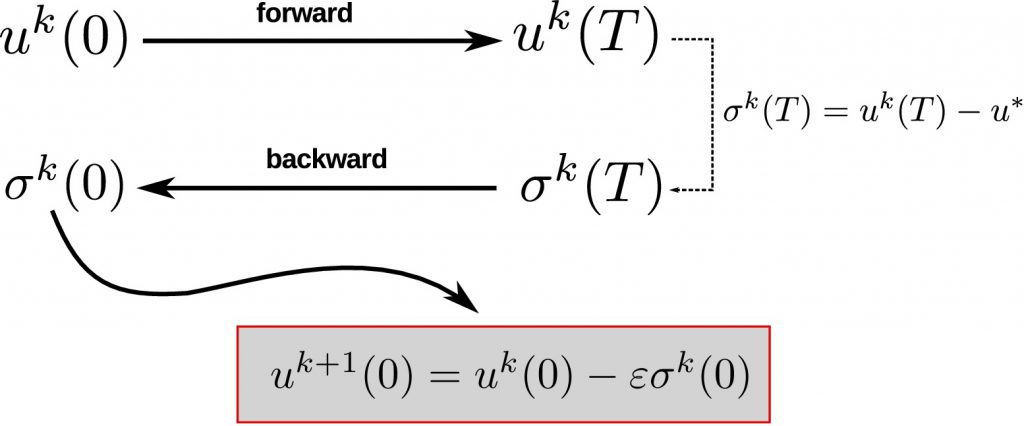
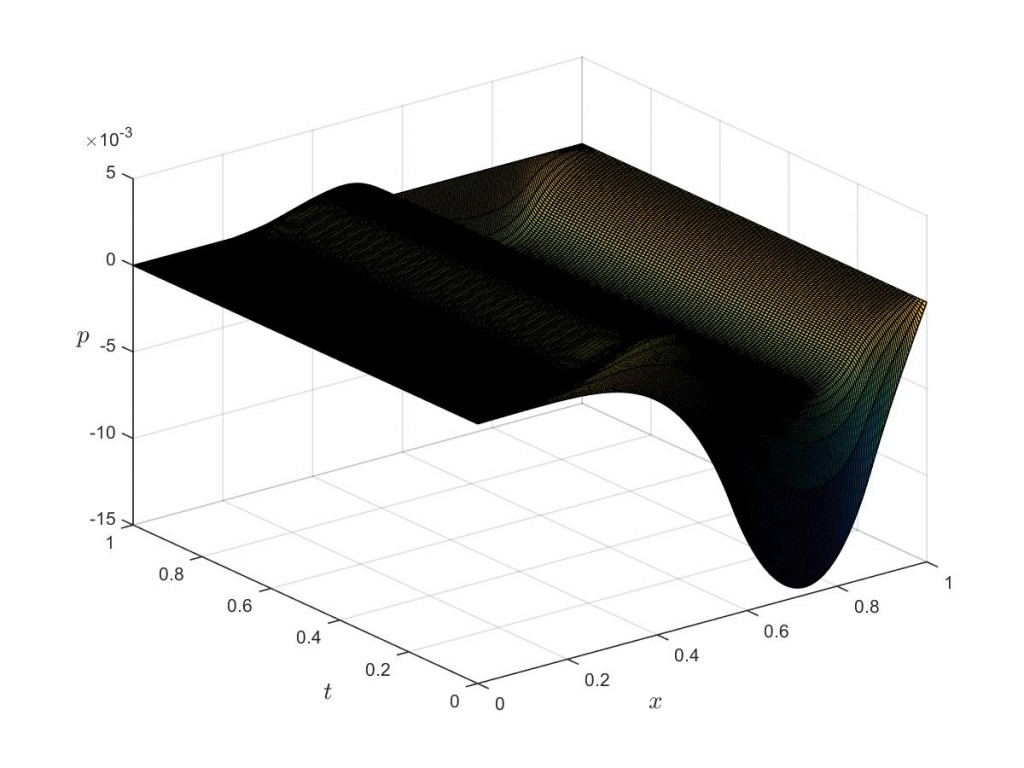
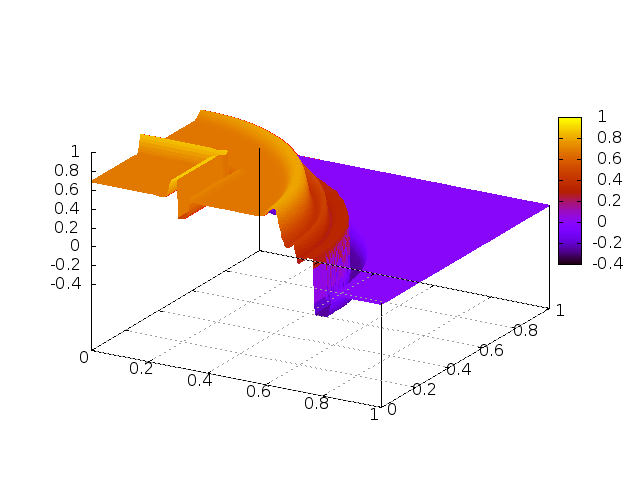
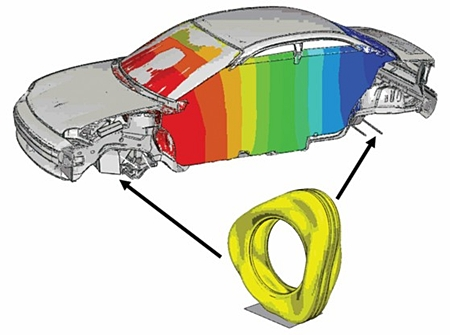
PDF version... 1. Adjoint estimation: low or high order? Adjoint methods have been systematically associated to the optimal control design [5] and their applications to aerodynamics [1, 4]. During the…
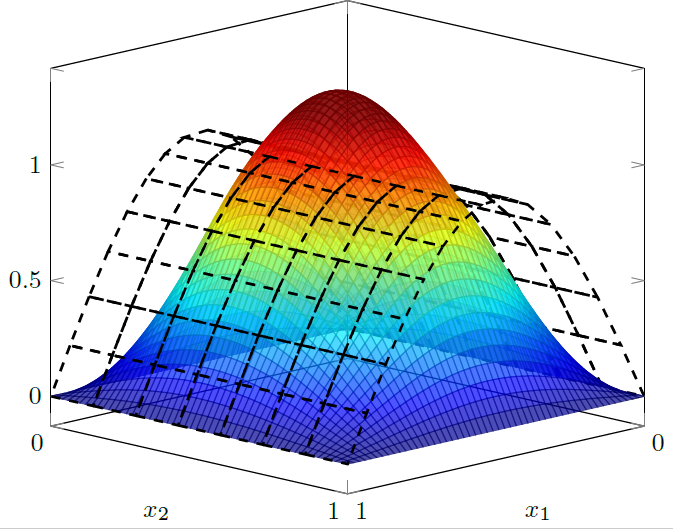
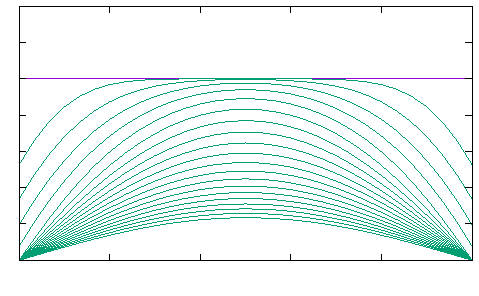
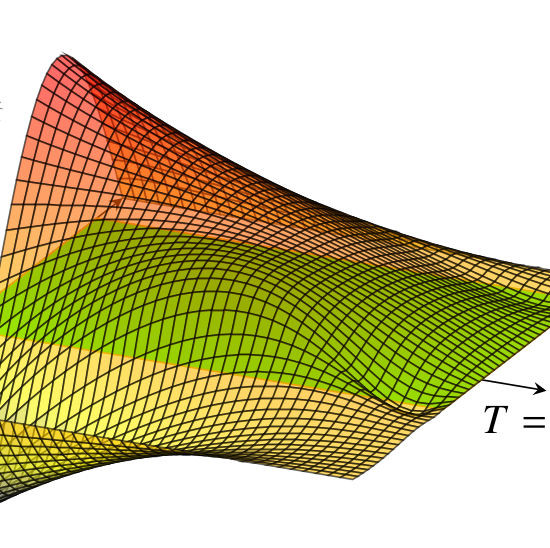
PDF version | Download Code... 1. Problem formulation Let $\Omega\subset \mathbb R^d$ be an open and bounded Lipschitz Domain and consider the parameter dependent parabolic equation with Dirichlet boundary conditions where…
"Diseño óptimo aeronaútico mediante técnicas novedosas". DOMINO, funded by MEC - From 2006 to 2009. (2006-2009) PI: ,
Funded by: European Science Foundation October 2008 - October 2013 More info at http://www.esf.org/optpde
Duration: January 2010 - December 2014
BFM2002-03345 - Funded by MCYT - From 01/01/2003 to 31/12/2005 (January 2003-December 2005) PI: , BFM2002-03345
MTM2005-00714 - Funded by MEC - From 01/01/2006 to 31/12/2008 (January 2006-December 2008) PI: , MTM2005-00714
(January 2009-December 2011) PI: , MTM2008-03541
PI2010-04 - Funded by Basque Government May 2010 - December 2012 PI: FP7-295217
Project reference: FP7-295217 Funded by REA_PEOPLE (IRSES) Duration: January 2012 - December 2014
Project reference: MTM2011-29306 Project financed by the MICINN through the VI I+D+i National Plan PI: Enrique Zuazua Research Center: BCAM (C02-01) - UPM (C02-02) Duration: January 2012 - December 2015 Workshops February…
Project reference: FA9550-14-1-0214 Funded by EOARD-AFOSR - UPMC (Paris) PI: Emanuel Trélat - Université Pierre et Marie Curie, Paris Duration: July 2014 - June 2017 FA9550-14-1-0214
Project reference: FA9550-15-1-0027 PI: M. Warma, Univ. Puerto Rico, Río Piedras, PR Host: AFOSR - Universidad de Puerto Rico Duration: December 2014 - November 2017
Project reference: MTM2014-52347 PI: Miguel Escobedo, J. C. Peral - UPV/EHU, Bilbao Funded by MINECO Duration: October 2015 - December 2017
This project aims at making a breakthrough contribution in the broad area of Control of Partial Differential Equations (PDE) and their numerical approximation methods by addressing some key issues that…
December 2015-December 2017 PI: E. Fdez. Cara, Universidad de Sevilla MTM2015-70444-REDT Web page of the event
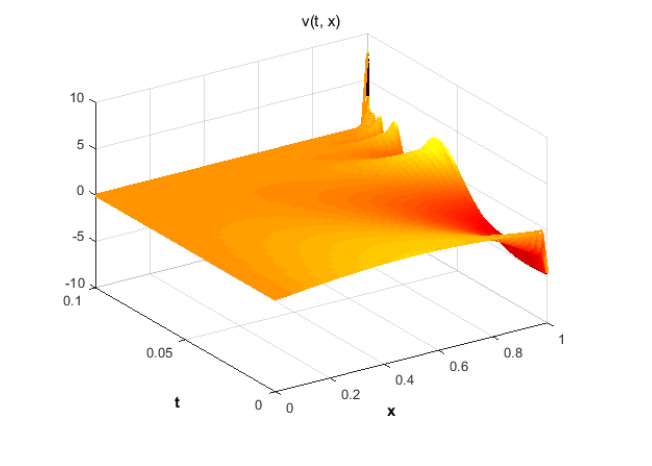
PDF version... | Download Code... Featured Video Evolution of the controls and of the state for $y^0=1$, $y^1=5$, $M=20$ and the discretization parameters $N_x=30$, $N_t=450$ in the minimal computed time $T\simeq\mathtt{0.2093}$.…
A finite element approximation of the one-dimensional fractional Poisson equation with applications to numerical control.
We want to study the following optimal control problem:
\begin{equation*}
\left(\mathcal{P}\right) \ \ \ \ \ \ \ \hat{u}\in\argmin_{u\in L^2_T} \left\{J\left(u\right)=\alpha_c \norm{u}_{1,T} + \frac{\beta}{2}\norm{u}^2_{T}+\alpha_s \norm{Lu}_{1,T} + \frac{\gamma}{2}\norm{Lu-z}_{T}^2\right\},
\end{equation*}
PDF version... The problem We analyze a model tracking problem for a 1D scalar conservation law. It consists in optimizing the initial datum so to minimize a weighted distance to…
This issue is motivated by the challenging problem of sonic-boom minimization for supersonic aircrafts, which is governed by a Burgers-like equation. The travel time of the signal to the ground is larger than the time scale of the initial disturbance by orders of magnitude and this motivates our study of large time control of the sonic-boom propagation...
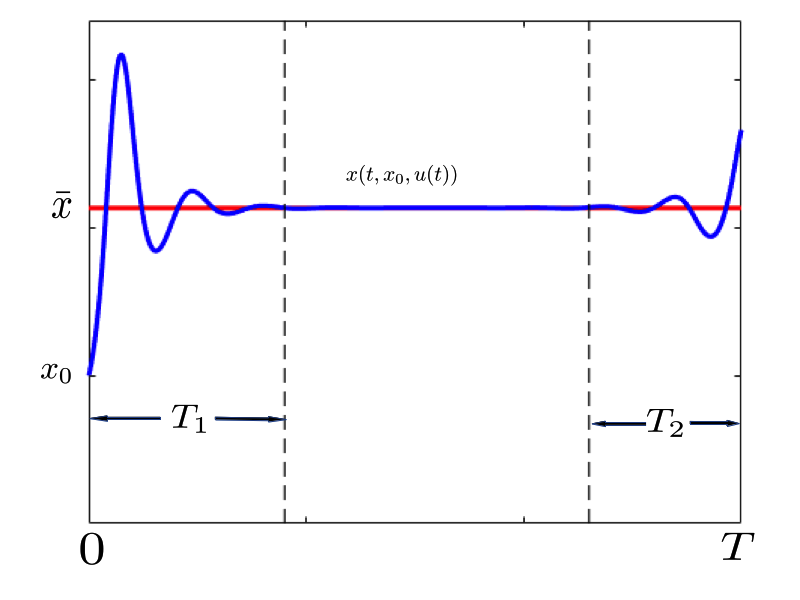
The turnpike property establishes that, when a general optimal control problem is settled in large time, for most of the time the optimal control and trajectories remain exponentially close to the optimal control and state of the corresponding steady-state or static optimal control problem...
Relevant models in Continuum Mechanics, Mathematical Physics and Biology are of non-local nature. Moreover, these models are applied for the description of several complex phenomena for which a local approach is inappropriate or limiting. In this setting, classical PDE theory fails because of non-locality. Yet many of the existing techniques can be tuned and adapted, although this is often a delicate matter...
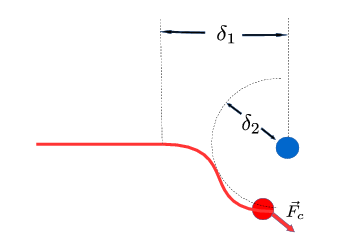
The standard approach for solving a driving problem is a leadership strategy, based on the attraction that a driver agent exerts on other agent. Repulsion forces are mostly used for collision avoidance, defending a target or describing the need for personal space. We present a “guidance by repulsion” model describing the behaviour of two agents, a driver and an evader...
Control of a parameter dependent system in a robust manner. Fix a control time $T > 0$, an arbitrary initial data $x^0$, and a final target $x^1 \in R^N$...
Our team has made several contributions in the description of the limit behaviour, as the mesh sizes tend to zero, of numerical schemes for wave and Schrödinger equations from a…
Control theory for PDEs has been quite exhaustively developed for model problems (heat and wave equations). But other important models in applications, of hybrid nature, remain poorly understood. This is…
Some important PDE models in Continuum Physics, such as hyperbolic conservation laws, represent a major challenge from a control viewpoint for two (closely related) reasons: solutions lack regularity properties and…
Most of the existing theory of controllability for PDEs has been developed in the absence of constraints on the controls and states. Thus, in practice, available results do not guarantee…
Control problems for evolution PDEs are most often considered in finite time intervals, without paying attention to the length of the control horizon and how it affects the nature of…
In real applications, models are not completely known since relevant parameters (deterministic or stochastic) are subject to uncertainty and indetermination. Accordingly, for practical purposes, robust analytical and computational methods are…
The Chair of Computational Mathematics is meant to hold projects related to various aspects of Applied Mathematics including Partial Differential Equations (PDE), Numerical Analysis, Control theory and Optimal Design. These interconnected fields have as goal the modelling, analysis, computer simulation and control and design of natural phenomena and engineering processes arising in several contexts of research, development and innovation (R+D+i)...