Sharp numerical approximation of the Hardy constant
L. Ignat, E. Zuazua (2025) Sharp numerical approximation of the Hardy constant Abstract. We study the P1 finite element approximation of the best constant in the classical Hardy inequality over…
Clustering in Pure-Attention Hardmax Transformers and its Role in Sentiment Analysis
A. Alcalde Zafra, G. Fantuzzi, E. Zuazua (2025) Clustering in Pure-Attention Hardmax Transformers and its Role in Sentiment Analysis, SIAM Mathematics of Data Science, SIMODS, arxiv: 2407.01602 Abstract. Transformers are…
A potential game perspective in Federated Learning
K. Liu, Z. Wang, E. Zuazua (2025) A potential game perspective in Federated Learning, arxiv:2411.11793 Abstract. Federated learning (FL) is an emerging paradigm for training machine learning models across distributed…
Optimal convergence rates for the finite element approximation of the Sobolev constant
L. Ignat, E. Zuazua (2025) Optimal convergence rates for the finite element approximation of the Sobolev constant Abstract. We establish optimal convergence rates for the P1 finite element approximation of…
Boundary observation and control for fractional heat and wave equations
U. Biccari, E. Zuazua (2025) Boundary observation and control for fractional heat and wave equations, https://doi.org/10.48550/arXiv.2504.17413 Abstract. We establish boundary observability and control for the fractional heat equation over arbitrary…
Turnpike in optimal control and beyond: A survey
E. Trélat, E. Zuazua (2025)Turnpike in optimal control and beyond: A survey https://hal.science/hal-05002039 Abstract. The turnpike principle is a fundamental concept in optimal control theory, stating that for a wide…
Representation and Regression Problems in Neural Networks: Relaxation, Generalization, and Numerics
K. Liu, E. Zuazua (2025) Representation and Regression Problems in Neural Networks: Relaxation, Generalization, and Numerics, Math. Models Methods Appl. Sci., Vol. 35, No. 6, pp. 1471-1521, arXiv:2412.01619v1, https://doi.org/10.1142/S0218202525500228 Abstract. In…
Exact Sequence Classification with Hardmax Transformers
A. Alcalde Zafra, G. Fantuzzi, E. Zuazua (2025) Exact Sequence Classification with Hardmax Transformers, arxiv: 2502.02270 Abstract. We prove that hardmax attention transformers perfectly classify datasets of $N$ labeled sequences…
On the decay of one-dimensional locally and partially dissipated and hyperbolic systems
T. Crin-Barat, N. De Nitti, E. Zuazua (2025) On the decay of one-dimensional locally and partially dissipated and hyperbolic systems, ESAIM:COCV, https://arxiv.org/abs/2206.00555 Abstract. We study the time-asymptotic behavior of linear…
Control of Hyperbolic and Parabolic Equations on Networks and Singular limits
J.A. Bárcena-Petisco, M. Cavalcante, G.M. Coclite, N. de Nitti, E. Zuazua (2025) Control of Hyperbolic and Parabolic Equations on Networks and Singular limits, MCRF, Vol. 15, No. 1, March 2025,…
FedADMM-InSa: An Inexact and Self-Adaptive ADMM for Federated Learning
Y. Song, Z. Wang, E. Zuazua (2025) FedADMM-InSa: An Inexact and Self-Adaptive ADMM for Federated Learning, Neural Networks, pp. 106-772, ISSN 0893-6080, https://doi.org/10.1016/j.neunet.2024.106772 Abstract. Federated learning (FL) is a promising…
Universal Approximation of Dynamical Systems by Semi-Autonomous Neural ODEs and Applications
Z. Li, K. Liu, L. Liverani, E. Zuazua (2025)Universal Approximation of Dynamical Systems by Semi-Autonomous Neural ODEs and Applications, arXiv: 2407.17092 Abstract. In this paper, we introduce semi-autonomous neural ordinary…
Deep Neural Networks: Multi-Classification and Universal Approximation
M. Hernandez, E. Zuazua (2025)Deep Neural Networks: Multi-Classification and Universal Approximation arXiv:2409.06555 Abstract. We demonstrate that a ReLU deep neural network with a width of 2 and a depth of…
Approximate and Weighted Data Reconstruction Attack in Federated Learning
Z. Wang, Y. Song, E. Zuazua (2025) Approximate and Weighted Data Reconstruction Attack in Federated Learning arXiv:2308.06822 Abstract. Federated Learning (FL) is a distributed learning paradigm that enables multiple clients…
Progress and future directions in machine learning through control theory
E. Zuazua (2024) Progress and future directions in machine learning through control theory Proceedings book FGS 2024, pp. 116, https://hdl.handle.net/10651/74677 Abstract. This paper presents our recent advancements at the intersection…
Stability and Convergence of a Randomized Model Predictive Control Strategy
D.W.M. Veldman, A. Borkowski, E. Zuazua (2024) Stability and Convergence of a Randomized Model Predictive Control Strategy , IEEE Trans. Automat., Vol. 69, No. 9, pp. 6253-6260 Abstract. This paper is…
Control of neural transport for normalising flows
D. Ruiz-Balet, E. Zuazua (2024)Control of neural transport for normalising flows J. Math. Pures Appl., Vol. 181, pp. 58-90, ISSN 0021-7824. https://doi.org/10.1016/j.matpur.2023.10.005 Abstract. Inspired by normalizing flows, we analyze the…
Optimal Placement and Shape Design of Sensors via Geometric Criteria
I. Ftouhi, E. Zuazua (2024) Optimal Placement and Shape Design of Sensors via Geometric Criteria, 2024 European Control Conference (ECC), Stockholm, Sweden, 2024, pp. 834-837, doi: 10.23919/ECC64448.2024.10591236 Abstract. The optimal…
Controllability properties from the exterior under positivity constraints for a 1-D fractional heat equation
H. Antil, U. Biccari, R. Ponce, M. Warma, S. Zamorano (2024) Controllability properties from the exterior under positivity constraints for a 1-D fractional heat equation, Vol. 13, pp. 893-924, https://doi.org/10.3934/eect.2024010…
DyCMaMod
DyCMaMod. Dinámica y control para el aprendizaje automático y la Modelización Project reference. PID2023-146872OB-I00 Funded by: MINECO. Ministerio de Economía, Comercio y Empresa Principal Investigator (PI): Prof. Enrique Zuazua, Prof.…
CoDeFeL. Control for Deep and Federated Learning
CoDeFeL: Control for Deep and Federated Learning ERC Advanced Grant 2022. Control for Deep and Federated Learning (CoDeFeL) Principal Investigator (PI): Prof. Enrique Zuazua Host Institution: Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU, Germany)…
Interplay between depth and width for interpolation in neural ODEs
A. Alvarez-Lopez, A. Hadj Slimane, E. Zuazua (2024) Interplay between depth and width for interpolation in neural ODEs, Neural Networks, Vol. 180, pp. 106-640, https://doi.org/10.1016/j.neunet.2024.106640, ISSN 0893-6080 Abstract. Neural ordinary…
Uniform Turnpike Property and Singular Limits
M Hernandez-Salinas, E. Zuazua (2024) Uniform Turnpike Property and Singular Limits Acta Appl. Math., Vol. 190, No. 3, https://doi.org/10.1007/s10440-024-00640-7 Abstract. Motivados por límites singulares para problemas de control óptimo a…
Large-time asymptotics in deep learning
C. Esteve, B. Geshkovski, D. Pighin, E. Zuazua (2025) Large-time asymptotics in deep learning, https://hal.archives-ouvertes.fr/hal-02912516 Abstract. We consider the neural ODE perspective of supervised learning and study the impact of the…
Reachable set for Hamilton-Jacobi equations with non-smooth Hamiltonian and scalar conservation laws
C. Esteve, E. Zuazua. Reachable set for Hamilton-Jacobi equations with non-smooth Hamiltonian and scalar conservation laws Nonlinear Analysis, Vol. 227, https://doi.org/10.1016/j.na.2022.113167 Abstract. We give a full characterization of the range…
Constrained control of gene-flow models
I. Mazari, D. Ruiz-Balet, E. Zuazua (2023)Constrained control of gene-flow models, Ann. Inst. Henri Poincare (C) Anal. Non Lineaire ⟨hal-02373668⟩ Abstract. In ecology and population dynamics, gene-flow refers to the transfer…
Multilevel control by duality
U. Biccari, E. Zuazua (2023) Multilevel control by duality Systems & Control Letters, Vol. 175, 105-502, https://doi.org/10.1016/j.sysconle.2023.105502 Abstract. We discuss the multilevel control problem for linear dynamical systems, consisting in designing…
Neural ODE Control for Classification, Approximation and Transport
D. Ruiz-Balet, E. Zuazua (2023)Neural ODE Control for Classification, Approximation and Transport, SIAM Review, Vol. 65, No. 3, pp. 735-773, https://doi.org/10.1137/21M1411433 Abstract. We analyze Neural Ordinary Differential Equations (NODEs) from…
Optimal design of sensors via geometric criteria
I. Ftouhi, E. Zuazua (2023) Optimal design of sensors via geometric criteria, J. Geom. Anal., Vol. 33, No. 253, https://doi.org/10.1007/s12220-023-01301-1 Abstract. We consider a convex set Ω and look for…
ERC DyCon project
DyCon: Dynamic Control is an European project funded by the European Research Council – ERC (2016 - 2022), focused at making a breakthrough contribution in the broad area of Control of Partial Differential Equations (PDE) and their numerical approximation methods by addressing key unsolved issues appearing systematically in real-life applications. The field of PDEs, together with numerical approximation, simulation methods and control theory, has evolved significantly to address the industrial demands.
Multiplicity of solutions for fractional q(.)-Laplacian equations
A. Rahmoune, U. Biccari (2023) Multiplicity of solutions for fractional -Laplacian equations., J Elliptic Parabol Equ, Vol. 9, pp. 1101–1129, https://doi.org/10.1007/s41808-023-00239-3 Abstract. In this paper, we deal with the following elliptic…
Multilevel Selective Harmonic Modulation via Optimal Control
U. Biccari, C. Esteve-Yagüe, D.J. Oroya-Villalta (2022) Multilevel Selective Harmonic Modulation via Optimal Control., Appl Math Optim, Vol. 86, No. 43, https://doi.org/10.1007/s00245-022-09917-5 Abstract. We consider the Selective Harmonic Modulation (SHM) problem,…
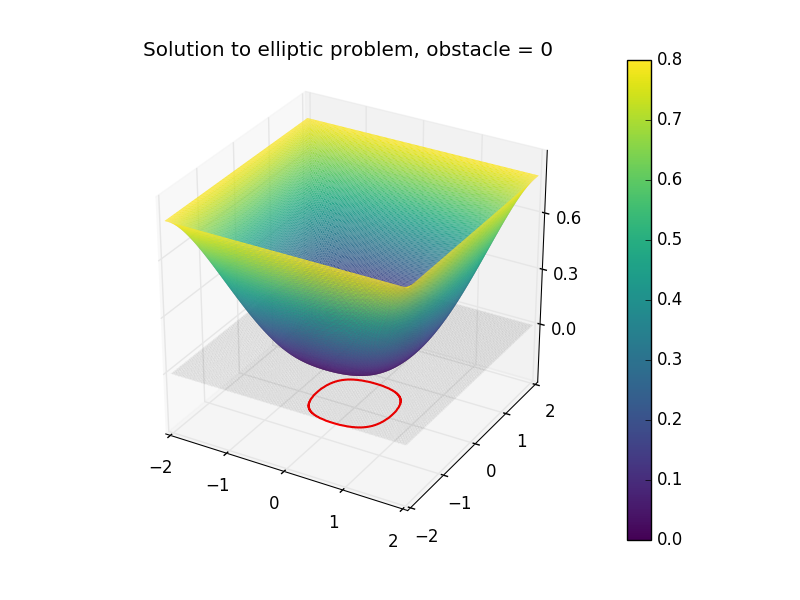
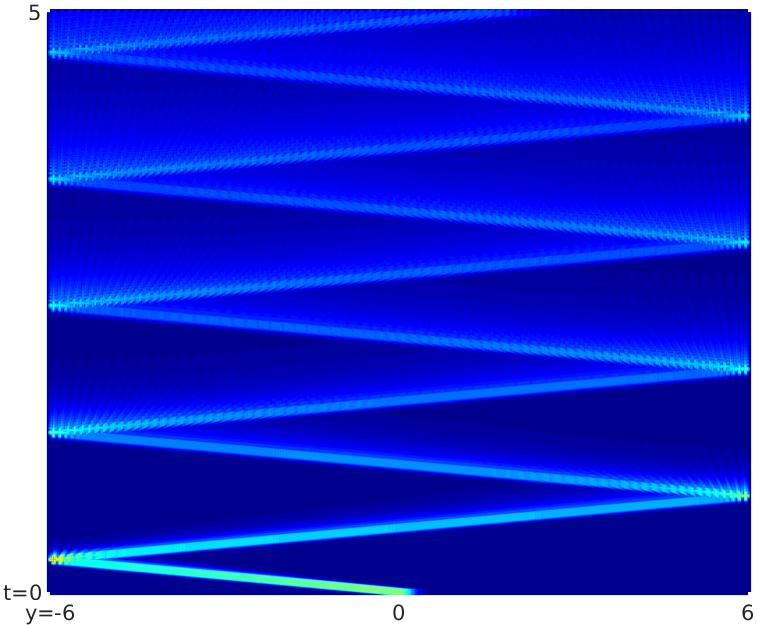
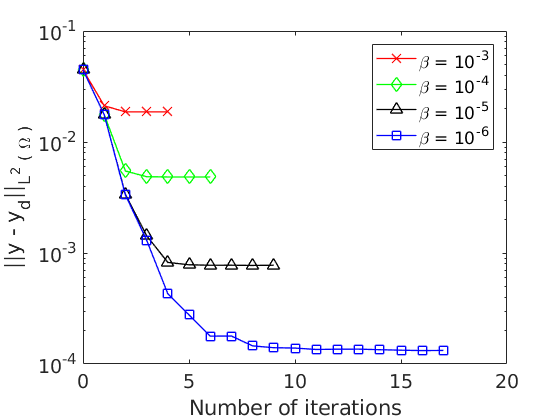
DASEL
Project name: DASEL, Ciencia de Datos para Redes Eléctricas Project reference: TED2021-131390B-I00 AEI: TED2021-131390B-I00/ AEI/10.13039/501100011033 DASEL Funding source: MINECO. Ministry of Science, Innovation and Universities. Proyectos de Transición Ecológica y…
Multilevel selective harmonic modulation by duality
U. Biccari, E. Zuazua Multilevel selective harmonic modulation by duality (2022) IFAC-PapersOnLine, Vol. 55, No. 16, pp. 56-61, https://doi.org/10.1016/j.ifacol.2022.08.081. Abstract. We address the Selective Harmonic Modulation (SHM) problem in power…
Differentiability with respect to the initial condition for Hamilton-Jacobi equations
C. Esteve, E. Zuazua. Differentiability with respect to the initial condition for Hamilton-Jacobi equations (2022) SIAM Journal on Mathematical Analysis, Vol. 54, No. 5, pp. 5388-5423 https://doi.org/10.1137/22M1469353 Abstract. We prove…
Control of certain parabolic models from biology and social sciences
Domènec Ruiz-Balet, , Enrique Zuazua. Control of certain parabolic models from biology and social sciences(2022) Math Control and Related Fields, Vol. 12, No. 4, pp 955-1038. doi: https://doi.org/10.3934/mcrf.2022032 Abstract. These…
Relaxation approximation and asymptotic stability of stratified solutions to the IPM equation
R. Bianchini, Crin-Barat T., M. Paicu. Relaxation approximation and asymptotic stability of stratified solutions to the IPM equation (2022) Abstract. We prove the nonlinear asymptotic stability of stably stratified solutions…
Diffusive Relaxation Limit of the Multi-Dimensional Hyperbolic Jin-Xin System
Crin-Barat T., L. Shou. Diffusive Relaxation Limit of the Multi-Dimensional Hyperbolic Jin-Xin System (2022) Abstract. In this paper we study the diffusive relaxation limit of the Jin-Xin system toward viscous…
KiLearn
Project name: KiLearn - Kinetic equations and Learning control Project reference: PID2020-112617GB-C22 AEI: PID2020-112617GB-C22/AEI/10.13039/501100011033 KiLearn Funding source: MINECO, Ministry of Science, Innovation and Universities Duration: September 2021 - May 2025…
A framework for randomized time-splitting in linear-quadratic optimal control
D.W.M. Veldman, E. Zuazua (2022) A framework for randomized time-splitting in linear-quadratic optimal control Numerische Mathematik, Vol. 151, No. 2, DOI: 10.1007/s00211-022-01290-3 Abstract. Inspired by the successes of stochastic algorithms in…
Nonuniqueness of minimizers for semilinear optimal control problems
D. Pighin. Nonuniqueness of minimizers for semilinear optimal control problems (2022) J. Eur. Math. Soc, , published online first. https://doi.org/10.4171/jems/1232 Abstract. A counterexample to uniqueness of global minimizers of semilinear…
The turnpike property and the longtime behavior of the Hamilton-Jacobi-Bellman equation for finite-dimensional LQ control problems
C. Esteve, H. Kouhkouh, D. Pighin, E. Zuazua. The turnpike property and the long-time behavior of the Hamilton-Jacobi-Bellman equation for finite-dimensional LQ control problems. Math. Control Signals Syst. (2022). https://doi.org/10.1007/s00498-022-00325-2 Abstract:…
Turnpike in Lipschitz-nonlinear optimal control
Esteve C., Geshkovski G., Pighin D., Zuazua E. . Turnpike in Lipschitz-nonlinear optimal control Nonlinearity. Vol 5. No. 34, pp. 1652-1701 (2022) https://doi.org/10.1088/1361-6544/ac4e61 Abstract. We present a new proof of…
The Vlasov-Fokker-Planck Equation with High Dimensional Parametric Forcing Term
Shi Jin, Yuhua Zhu, Enrique Zuazua. The Vlasov-Fokker-Planck Equation with High Dimensional Parametric Forcing Term Numer. Math. 150, 479–519 (2022). https://doi.org/10.1007/s00211-021-01257-w Abstract. We consider the Vlasov-Fokker-Planck equation with random electric…
Model predictive control with random batch methods for a guiding problem
Ko Dongnam, Zuazua Enrique. Model predictive control with random batch methods for a guiding problem (2021). Math. Models Methods Appl. Sci., Vol. 31, No. 8, pp. 1569-1592. (2021) DOI: https://doi.org/10.1142/S0218202521500329…
Classical system theory revisited for Turnpike in standard state space systems and impulse controllable descriptor systems
Heiland J., Zuazua E. Classical system theory revisited for Turnpike in standard state space systems and impulse controllable descriptor systems (2021) SIAM J. Control Optim., Vol. 59.5 (2021), pp. 3600-3624 Abstract.…
Optimal control for neural ODE in a long time horizon and applications to the classification and simultaneous controllability problems
Jon Asier Bárcena-Petisco. Optimal control for neural ODE in a long time horizon and applications to the classification (2021) Abstract. We study the optimal control in a long time horizon…
Local null controllability of the penalized Boussinesq system with a reduced number of controls
J.A. Bárcena-Petisco, Kevin Le Balc'H. Local null controllability of the penalized Boussinesq system with a reduced number of controls (2021) Abstract. In this paper we consider the Boussinesq system with homogeneous…
Controllability of one-dimensional viscous free boundary flows
B. Geshkovski, E. Zuazua. Controllability of one-dimensional viscous free boundary flows. Siam. J. Control. Optim (2021), Vol. 59, No. 3, pp. 1830–1850. https://doi.org/10.1137/19M1285354 Abstract. In this work, we address the…
The turnpike property in semilinear control
D. Pighin The turnpike property in semilinear control ESAIM Control Optim. Calc. Var., Vol. 26 (2021), pp. 1-48 Abstract.An exponential turnpike property for a semilinear control problem is proved. The…
DyCon blog: Multilevel Selective Harmonic Modulation via Optimal Control
Spain. 12.04.2021. Our team members Deyviss Jesús Oroya-Villalta, Carlos Esteve-Yagüe and Umberto Biccari, made a contribution to the DyCon Blog about "Multilevel Selective Harmonic Modulation via Optimal Control": Selective harmonic Modulation (SHM)…
The Finite-Time Turnpike Phenomenon for Optimal Control Problems: Stabilization by Non-smooth Tracking Terms
M. Gugat, M. Schuster, E. Zuazua. The Finite-Time Turnpike Phenomenon for Optimal Control Problems: Stabilization by Non-Smooth Tracking Terms, in "Stabilization of Distributed Parameter Systems: Design Methods and Applications". Grigory…
Local null controllability of a model system for strong interaction between internal solitary waves
Jon Asier Bárcena-Petisco, Sergio Guerrero and Ademir F. Pazoto. Local null controllability of a model system for strong interaction between internal solitary waves. Commun. Contemp. Math. (2021) https://doi.org/10.1142/S0219199721500036 Abstract. In…
DyCon blog: Points of Interest Extraction and Prediction of Next Locations
Spain. 10.03.2021. Aicha Karite recent member from our team, made a contribution to the DyCon Blog about "Points of Interest Extraction and Prediction of Next Locations": Generally, a prediction problem…
Control and Deep Learning: Some connections
B. Geshkovski, E. Zuazua. Control and Deep Learning: Some connections (2021) This note is an extended abstract for a talk given by the second author during the workshop ”Challenges in…
Internal control for a non-local Schrödinger equation involving the fractional Laplace operator
U. Biccari Internal control for a non-local Schrödinger equation involving the fractional Laplace operator (2022), Vol. 11, No. 1: 301-324. doi: 10.3934/eect.2021014 Abstract: We analyze the interior controllability problem for…
Nonnegative control of finite-dimensional linear systems
Lohéac J., Trélat E., Zuazua E. Nonnegative control of finite-dimensional linear systems. Ann. I. H. Poincare-An., Vol. 38, No. 2, pp. 301-346. (2021) DOI: https://doi.org/10.1016/j.anihpc.2020.07.004 Abstract. We consider the controllability…
Rotor imbalance suppression by optimal control
M. Gnuffi, D. Pighin, N. Sakamoto Rotor imbalance suppression by optimal control Optimal Control Applications and Methods, Vol. 43, No. 1 (2022), pp. 213-242. Abstract. An imbalanced rotor is considered.…
DyCon blog: Averaged dynamics and control for heat equations with random diffusion
Spain. 04.12.2020. Our team member Jon Asier Bárcena Petisco and our Head Enrique Zuazua made a contribution to the DyCon Blog about "Averaged dynamics and control for heat equations with…
The Inverse Problem for Hamilton-Jacobi equations and Semiconcave Envelopes
Esteve C., Zuazua E.. The Inverse Problem for Hamilton-Jacobi equations and Semiconcave Envelopes SIAM J. Math. Anal., Vol. 52, No. 6, pp. 5627–5657 (2020). https://doi.org/10.1137/20M1330130 Abstract. We study the inverse…
Null-controllability of perturbed porous medium gas flow
B. Geshkovski,Null-controllability of perturbed porous medium gas flow. ESAIM:COCV, vol. 26, No. 85 (2020). DOI: 10.1051/cocv/2020009 Abstract: In this work, we investigate the null-controllability of a nonlinear degenerate parabolic equation,…
DyCon blog: Q-learning for finite-dimensional problems
Spain. 29.10.2020. Our team member Carlos Esteve made a contribution to the DyCon Blog about "Q-learning for finite-dimensional problems": Reinforcement Learning (RL) is, together with Supervised Learning and Unsupervised Learning,…
Control under constraints for multi-dimensional reaction-diffusion monostable and bistable equations
Ruiz-Balet D., Zuazua E.. Control under constraints for multi-dimensional reaction-diffusion monostable and bistable equations. J. Math. Pures Appl, vol. 143, pp. 345-375 (2020) https://doi.org/10.1016/j.matpur.2020.08.006 Abstract. Dynamic phenomena in social and…
Sparse source identification of linear diffusion–advection equations by adjoint methods
Monge A., Zuazua E. Sparse source identification of linear diffusion–advection equations by adjoint methods. Syst. Control. Lett, vol. 145 (2020). DOI: https://doi.org/10.1016/j.sysconle.2020.104801 Abstract: We present an algorithm for the time-inversion…
The turnpike with lack of observability
Pighin D., Sakamoto N. The turnpike with lack of observability (2020) Abstract: We obtain turnpike results for optimal control problems with lack of stabilizability in the state equation and/or detectability in…
Controllability of a Class of Infinite Dimensional Systems with Age Structure
Maity D., Tucsnak M., Zuazua E. Controllability of a Class of Infinite Dimensional Systems with Age Structure. Control Cybern. Vol. 48 (2020), No. 2, pp. 231-260 hal-01964612v2 Abstract: Given a…
Shape turnpike for linear parabolic PDE models
Lance G., Trélat E., Zuazua E. Shape turnpike for linear parabolic PDE models Syst. Control. Lett. Vol. 142 (2020). DOI: 10.1016/j.sysconle.2020.104733 Abstract: We introduce and study the turnpike property for…
A stochastic approach to the synchronization of coupled oscillators
Umberto Biccari, Enrique Zuazua. A stochastic approach to the synchronization of coupled oscillators. Frontiers in Energy Research, section Smart Grids. Front. Energy Res. Vol. 8 (2020). DOI: 10.3389/fenrg.2020.00115 Abstract. This paper…
Full probabilistic solution of a infinite dimensional linear control system with random initial and final conditions
J.-C. Cortes, A. Navarro-Quiles, J.-V. Romero, M.-D. Rosello, E. Zuazua. Full probabilistic solution of a infinite dimensional linear control system with random initial and final conditions. J. Franklin I. (2020)…
Turnpike in optimal shape design
G. Lance, E. Trélat, E. Zuazua Turnpike in optimal shape design IFAC-PapersOnline, Vol. 52, No. 16 (2019), pp. 496-501, ISSN: 24058963, DOI: 10.1137/17M1119160 Abstract: We investigate the turnpike problem in…
Stochastic optimization methods for the simultaneous control of parameter-dependent systems
Umberto Biccari, Ana Navarro-Quiles, Enrique Zuazua. Stochastic optimization methods for the simultaneous control of parameter-dependent systems (2020) Abstract. We address the application of stochastic optimization methods for the simultaneous control of…
Asymptotic behavior and control of a “guidance by repulsion” model
Dongnam Ko, E. Zuazua, Asymptotic behavior and control of a "guidance by repulsion" model. Math Models Methods Appl. Sci. Vol. 30, No. 04, pp. 765-804 (2020).DOI:10.1142/S0218202520400047 Abstract. We model and…
Stochastic persistency of nematic alignment state for the Justh-Krishnaprasad model with additive white noises
Seung-Yeal Ha, Dongnam Ko, Woojoo Shim, Hui Yu, . Stochastic persistency of nematic alignment state for the Justh-Krishnaprasad model with additive white noises. Math Models Methods Appl. Sci. Vol. 30,…
The turnpike property in nonlinear optimal control – A geometric approach
N. Sakamoto, D. Pighin, E. Zuazua The turnpike property in nonlinear optimal control - A geometric approach. IEEE 58th Conference on Decision and Control (CDC) (2020). DOI: 10.1109/CDC40024.2019.9028863 Abstract: This paper…
Controllability of the one-dimensional fractional heat equation under positivity constraints
U. Biccari, M. Warna, E. Zuazua Internal observability for coupled systems of linear partial differential equations. Commun. Pure Appl. Anal., Vol 19. No. 4 (2019), pp. 1949-1978. DOI: 10.3934/cppaa.2020086
CONVADP
Project name: CONVADP Project reference: CONVADP Funding source: ELKARTEK - Basque Government Duration: March 2020 - December 2021 Principal Investigator (PI): Umberto Biccari About the Project CONVADP is a collaborative…
A fragmentation phenomenon for a non-energetic optimal control problem: optimisation of the total population size in logistic diffusive models
I. Mazari, D. Ruiz-Balet. A fragmentation phenomenon for a non-energetic optimal control problem: optimisation of the total population size in logistic diffusive models (2020) Abstract. Following the recent works [9, 17,…
DyCon blog: Inverse problem for Hamilton-Jacobi equations
Spain. 03.04.2020. Today, our team member Carlos Esteve made a contribution to the DyCon Blog about "Inverse problem for Hamilton-Jacobi equations": Inverse design problem for Hamilton-Jacobi equations: projection on the…
Asymptotic behavior of scalar convection-diffusion equations
Enrique Zuazua. Asymptotic behavior of scalar convection-diffusion equations (2020) Abstract. In these lecture notes, we address the problem of large-time asymptotic behaviour of the solutions to scalar convection-diffusion equations set in…
DyCon Blog: POD and DMD Reduced Order Models for a 2D Burgers Equation
Spain. 11.03.2020. Today, our team member Jan Heiland made a contribution to the DyCon Blog about "POD and DMD Reduced Order Models for a 2D Burgers Equation": "The DMD approach…
A PDE-ODE model for traffic control with autonomous vehicles
Thibault Liard, Raphael Stern, Maria Laura Delle Monache. A PDE-ODE model for traffic control with autonomous vehicles. (2020) Abstract. We introduce a coupled PDE-ODEs model to describe mixed traffic with…
Emergent collective behaviors of stochastic kuramoto oscillators
Seung-Yeal Ha, Dongnam Ko, Chanho Min, Xiongtao Zhang. Emergent collective behaviors of stochastic kuramoto oscillators. Vol. 25, No. 3, pp. 1059-1081 (2020) DOI: 10.3934/dcdsb.2019208 Abstract. We study the collective dynamics…
DyCon Blog: Stabilization of a double pendulum on a cart with DyCon Toolbox
Spain. 14.02.2020. Yesterday, our team members Jesús Oroya and Jorge Mallo made a contribution to the DyCon Blog about "Stabilization of a double pendulum on a cart with DyCon Toolbox".…
Null-controllability properties of a fractional wave equation with a memory term
U. Biccari, M. Warma Null-controllability properties of a fractional wave equation with a memory term. Evol. Eq. Control The., Vol. 9, No. 2 (2020), pp. 399-430 Abstract: We study the…
Existence and cost of boundary controls for a degenerate/singular parabolic equation
U. Biccari, V. Hernandez-Santamaria, J. Vancostenoble. Existence and cost of boundary controls for a degenerate/singular parabolic equation (2022). Mathematical Control and Related Fields, Vol. 12, No.2, pp. 495-530, doi: 10.3934/mcrf.2021032…
Propagation of one and two-dimensional discrete waves under finite difference approximation
U. Biccari, A. Marica, E. Zuazua Propagation of one and two/dimensional discrete waves under finite difference approximation, Found. Comput. Math., Vol. 20 (2020), pp. 1401-1438. DOI: 10.1007/s10208-020-09445-0 Abstract: We analyze…
Output controllability in a long-time horizon
Martin Lazar, Jerôme Lohéac. Output controllability in a long-time horizon. Automatica, Vol. 113 (2020). DOI: 10.1016/j.automatica.2019.108762 Abstract. In this article we consider a linear finite dimensional system. Our aim is…
A controlled multiscale model for traffic regulation via autonomous vehicles
T. Liard, . A controlled multiscale model for traffic regulation via autonomous vehicles. (2019) Abstract. Autonomous vehicles ($AV$s) allow new ways of regulating the traffic flow on road networks. Most…
On entropic solutions to conservation laws coupled with moving bottlenecks
T. Liard, Benedetto Piccoli. On entropic solutions to conservation laws coupled with moving bottlenecks. (2019) Abstract. Moving bottlenecks in road traffic represent an interesting mathematical problem, which can be modeled…
Optimal driving strategies for traffic control with autonomous vehicles
T. Liard, Raphael Stern, Maria Laura Delle Monache. Optimal driving strategies for traffic control with autonomous vehicles. IFAC-PapersOnLine 53.2 (2020), pp. 5322-5329 Abstract. This article considers the possibility of using…
Inverse design for the one-dimensional Burgers equation
T. Liard, E. Zuazua. Inverse design for the one-dimensional Burgers equation. (2019) Abstract. In this paper, we study the problem of inverse design for the one-dimensional Burgers equation. This problem…
Single-point Gradient Blow-up on the Boundary for Diffusive Hamilton-Jacobi Equation in domains with non-constant curvature
C. Esteve Single-point Gradient Blow-up on the Boundary for Diffusive Hamilton-Jacobi Equation in domains with non-constant curvatureJ MATH PURE APPL, Vol 137 (2020) pp. 143-177, DOI: 10.1016/j.matpur.2019.12.006 Abstract. We consider…
DyCon blog: Analysis, numerics and control for the obstacle problem
Spain. 15.09.2019. Today, our team member Borjan Geshkovski made a contribution to the DyCon Blog about "Analysis, numerics and control for the obstacle problem": In this tutorial, we present some…
Model reduction of converter-dominated power systems by Singular Perturbation Theory
U. Biccari, N. Sakamoto, E. Unamuno, D. Madariaga, E. Zuazua, J.A. Barrena. Model reduction of converter-dominated power systems by Singular Perturbation Theory Abstract: The increasing integration of power electronic devices is driving the development of more advanced tools and methods for…
DyCon blog
If you are looking for our DyCon ERC project output, don't miss out: Our DyCon Toolbox for computational methods and tools Our DyCon blog for our last dissemination posts about…
Turnpike in optimal shape design for heat equation
G. Lance, E. Trélat, E. Zuazua Turnpike in optimal shape design for heat equation (2019) IFAC-PAPERSONLINE, Vol. 52, No. 16, pp. 496-501, DOI: 10.1137/17M1119160 Abstract: After a short presentation of…
Road2DC: New Tools for the Design and Control of Hybrid ac/dc Distribution Networks
Project financed by the Basque Government (ELKARTEK programme). Principal Investigator: Jon Andoni Barrena DeustoTech - CCM Coordinator: Enrique Zuazua Iriondo Research Centers: Mondragon University, CCM & Energy (DeustoTech), TECNALIA, Ingeteam & IK4-IKERLAN. Duration: January 2018 - December…
ERC – DyCon: Dynamic Control Project
Funded by ERC - European Research Council Project Acronym: DyConProject Full Title: Dynamic Control and Numerics of Partial Differential Equations Project reference: 694126Principal Investigator: Enrique ZuazuaHost Institutions: DeustoTech - Deusto…
Nonlocal PDEs: Analysis, Control and Beyond
"Nonlocal PDEs: Analysis, Control and Beyond" PI: M. Warma FA9550-18-1-0242, AFOSR - University of Puerto Rico - From June 2018 to May 2021. More information