Spain. 04.12.2020. Our team member Jon Asier Bárcena Petisco and our Head Enrique Zuazua made a contribution to the DyCon Blog about “Averaged dynamics and…
View More DyCon blog: Averaged dynamics and control for heat equations with random diffusion
Category: WP1-PDC
WP1: Control of Parameter Dependent Problems (PDC)
Full probabilistic solution of a infinite dimensional linear control system with random initial and final conditions
J.-C. Cortes, A. Navarro-Quiles, J.-V. Romero, M.-D. Rosello, E. Zuazua. Full probabilistic solution of a infinite dimensional linear control system with random initial and final…
View More Full probabilistic solution of a infinite dimensional linear control system with random initial and final conditionsStochastic optimization methods for the simultaneous control of parameter-dependent systems
Umberto Biccari, Ana Navarro-Quiles, Enrique Zuazua. Stochastic optimization methods for the simultaneous control of parameter-dependent systems (2020) Abstract. We address the application of stochastic optimization methods…
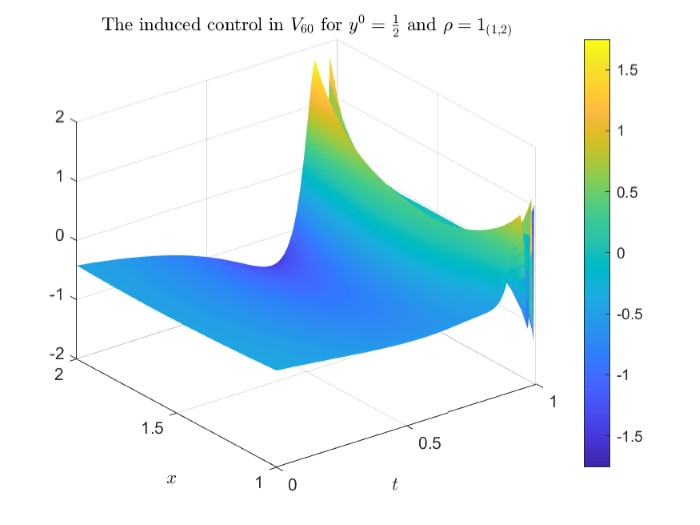
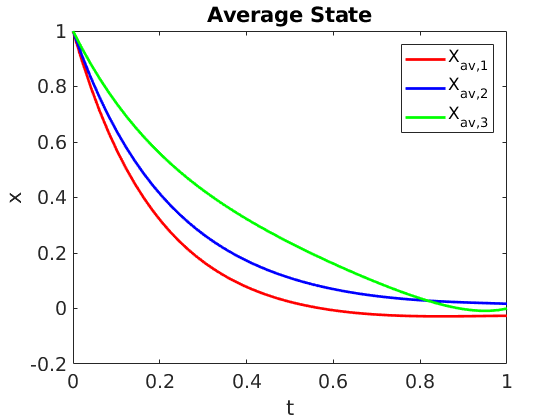
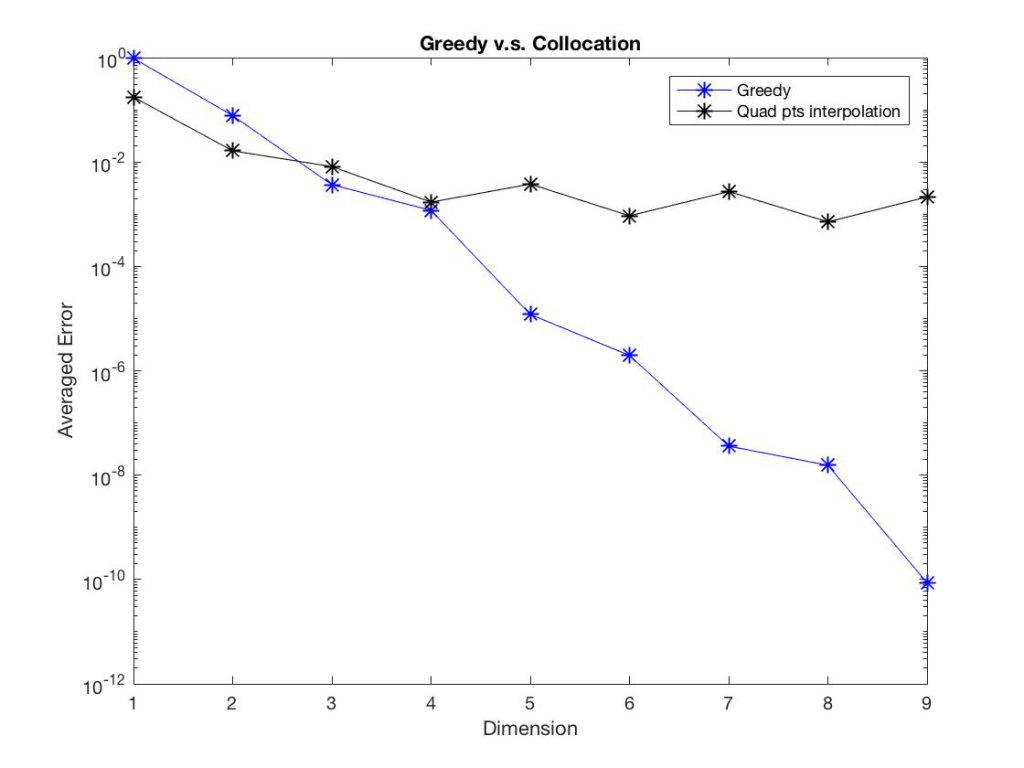
View More Stochastic optimization methods for the simultaneous control of parameter-dependent systemsThe Vlasov-Fokker-Planck Equation with High Dimensional Parametric Forcing Term
Shi Jin, Yuhua Zhu, Enrique Zuazua. The Vlasov-Fokker-Planck Equation with High Dimensional Parametric Forcing Term Abstract. We consider the Vlasov-Fokker-Planck equation with random electric field…
View More The Vlasov-Fokker-Planck Equation with High Dimensional Parametric Forcing TermAveraged Control SCILAB code
Download Code related to the Averaged control problem.
Developed by Víctor Hernández-Santamaría, José Vicente Lorenzo & Enrique Zuazua.
Greedy optimal control for elliptic problems and its application to turnpike problems MATLAB code
Download Code related to the Greedy optimal control for elliptic problems and its application to turnpike problems problem.
Developed by Victor Hernández-Santamaría, Martin Lazar & Enrique Zuazua.
Averaged Control
PDF version | Download Matlab Code | Download Scilab Code | GITHUB In this work, we address the optimal control of parameter-dependent systems. We introduce…
View More Averaged ControlAveraged control MATLAB code
Download Code related to the Averaged control problem.
Developed by Víctor Hernández-Santamaría, José Vicente Lorenzo & Enrique Zuazua.
Wavecontrol MATLAB code
Download Code related to Wavecontrol.
Developed by C. Castro, M. Cea, S. Micu, A. Munch, M. Negreanu & Enrique Zuazua.