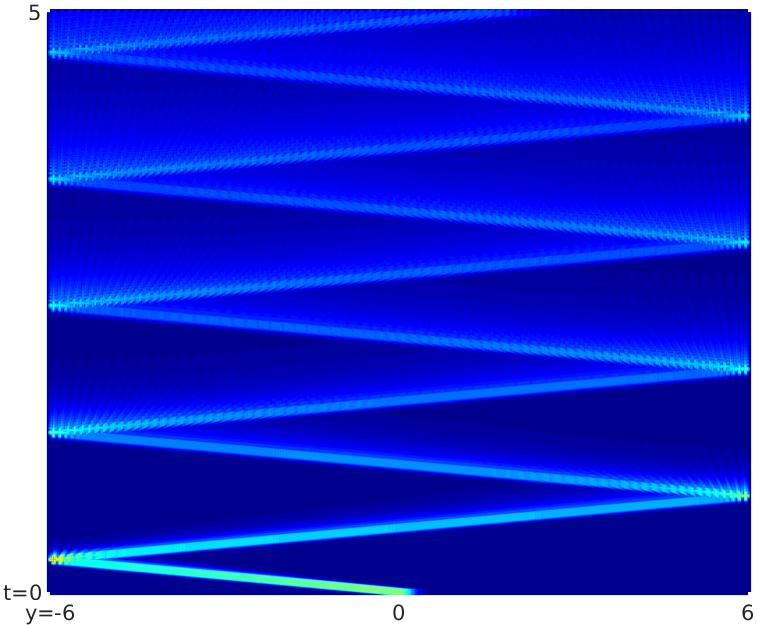
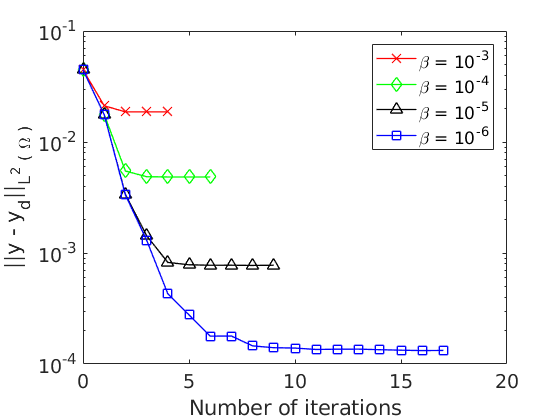
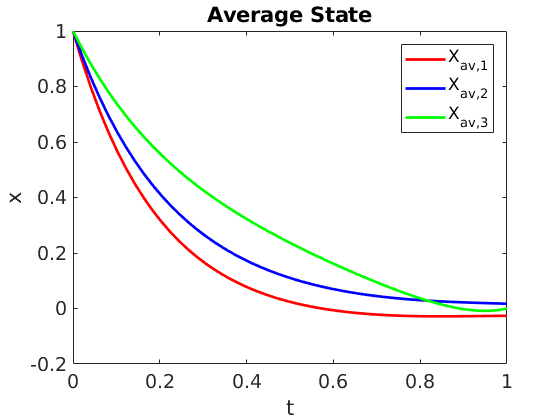
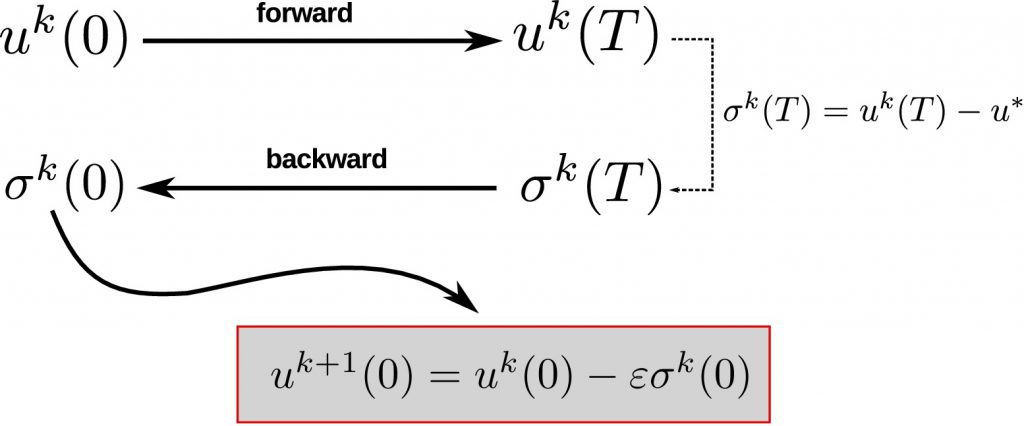
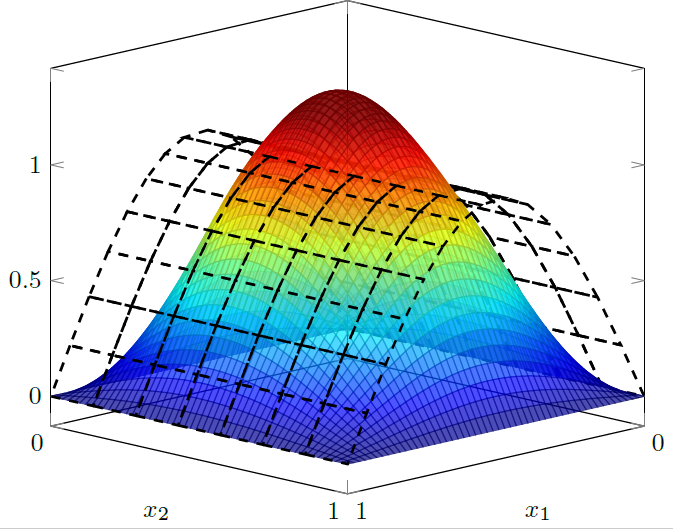
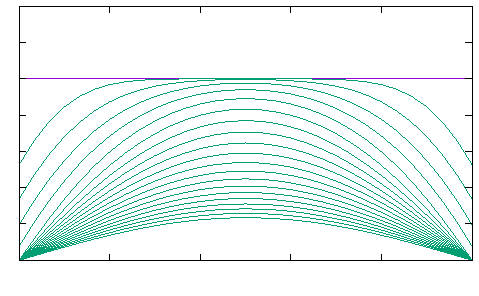
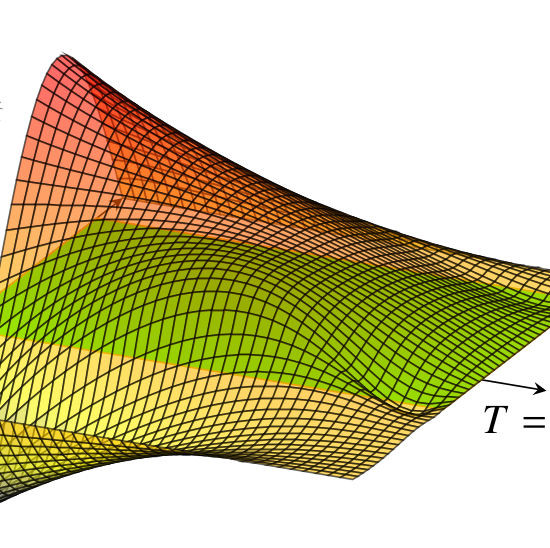
Control of certain parabolic models from biology and social sciences
Domènec Ruiz-Balet, , Enrique Zuazua. Control of certain parabolic models from biology and social sciences(2022) Math Control and Related Fields, Vol. 12, No. 4, pp 955-1038. doi: https://doi.org/10.3934/mcrf.2022032 Abstract. These…