Publications – Page 2 – cmc.deusto.eus

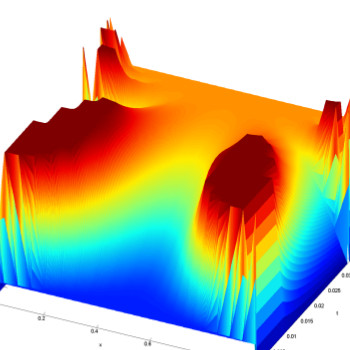
Quantitative touchdown localization for the MEMS problem with variable dielectric permittivity

C. Esteve, Ph Souplet. Quantitative touchdown localization for the MEMS problem with variable dielectric permittivity, NONLINEARITY, Vol. 31, No. 11 (2018). DOI: 10.1088/1361-6544 Abstract. We consider a well-known model for…

The evolution problem associated with eigenvalues of the Hessian

P. Blanc, C. Esteve, J. D. Rossi. The evolution problem associated with eigenvalues of the Hessian. J. London Math. Soc. (2020). https://doi.org/10.1112/jlms.12363 Abstract. In this paper we study the evolution…

Single-point Gradient Blow-up on the Boundary for Diffusive Hamilton-Jacobi Equation in domains with non-constant curvature

C. Esteve Single-point Gradient Blow-up on the Boundary for Diffusive Hamilton-Jacobi Equation in domains with non-constant curvatureJ MATH PURE APPL, Vol 137 (2020) pp. 143-177, DOI: 10.1016/j.matpur.2019.12.006 Abstract. We consider…

No touchdown at points of small permittivity and nontrivial touchdown sets for the MEMS problem

C. Esteve, Ph. Souplet, No touchdown at points of small permittivity and nontrivial touchdown sets for the MEMS problem Adv. Differential Equ. Vol. 24, No. 7/8 (2019), pp. 465-500 https://projecteuclid.org/euclid.ade/1556762456…

Controllability properties from the exterior under positivity constraints for a 1-D fractional heat equation

Antil H, Biccari U, Ponce R, Warma M, Zamorano S. Controllability properties from the exterior under positivity constraints for a 1-D fractional heat equation Abstract. We study the controllability to…

Model reduction of converter-dominated power systems by Singular Perturbation Theory

U. Biccari, N. Sakamoto, E. Unamuno, D. Madariaga, E. Zuazua, J.A. Barrena. Model reduction of converter-dominated power systems by Singular Perturbation Theory Abstract: The increasing integration of power electronic devices is driving the development of more advanced tools and methods for…

Adjoint computational methods for 2D inverse design of linear transport equations on unstructured grids

M. Morales-Hernández, E. Zuazua Adjoint computational methods for 2D inverse design of linear transport equations on unstructured grids Comp. Appl. Math. Vol. 38, No. 168 (2019) DOI: 10.1007/s40314-019-0935-0 Abstract: We address…

Null controllability of a nonlocal heat equation with an additive integral kernel

U. Biccari, V. Hernández-Santamaría Null controllability of a nonlocal heat equation with an additive integral kernel. SIAM J. Control Optim., Vol. 57, No. 4 (2019), pp. 2924-2938, DOI: 10.1137/18M1218431 Abstract:…

Spectral shape optimization for the Neumann traces of the Dirichlet-Laplacian eigenfunctions

released

Y. Privat, E. Trélat & E. Zuazua. Spectral shape optimization for the Neumann traces of the Dirichlet-Laplacian eigenfunctions. CALC VAR PARTIAL DIF. Springer Verlag, Vol. 58, No. 2 (2019) pp.…

Null-controllability properties of the wave equation with a second order memory term

U. Biccari, S. Micu Null-controllability properties of the wave equation with a second order memory termJ DIFFER EQUATIONS, Vol. 267, No. 2 (2019), pp. 1376-1422 doi.org/10.1016/j.jde.2019.02.009 Abstract: We study the…

Dynamics and control for multi-agent networked systems: a finite difference approach

released

U. Biccari, D. Ko, E. Zuazua Dynamics and control for multi-agent networked systems: a finite difference approach. Math. Models Methods Appl. Sci., Vol. 29, No. 4 (2019), pp. 755–790. DOI:…

Phase portrait control for 1D monostable and bistable reaction-diffusion equations

Pouchol C., Trélat E., Zuazua E. Phase portrait control for 1D monostable and bistable reaction-diffusion equations. Nonlinearity, Vol. 32, No. 3 (2019). DOI: 10.1088/1361-6544/aaf07e Abstract: We consider the problem of…

A probabilistic analysis of a Beverton-Holt type discrete model: Theoretical and computing analysis

J.-C. Cortés, A. Navarro-Quiles, J.-V. Romero, M.-D. Roselló A probabilistic analysis of a Beverton-Holt type discrete model: Theoretical and computing analysis . COMPUT MATH METHOD M. Vol. 1, No. 1…

A parabolic approach to the control of opinion spreading

released

D. Ruiz-Balet, E. Zuazua A parabolic approach to the control of opinion spreading. In: Berezovski A., Soomere T. (eds) Applied Wave Mathematics II. Mathematics of Planet Earth, Vol 6. Springer,…

Internal observability for coupled systems of linear partial differential equations

Lissy, P., Zuazua, E. Internal observability for coupled systems of linear partial differential equations , SIAM J. Control Optim., Vol. 57, No. 2 (2019), pp. 832–853. DOI: 10.1137/17M1119160 Abstract: We…

A Two-Dimensional “Flea on the Elephant” Phenomenon and its Numerical Visualization

Bianchini, R., Gosse, L., Zuazua, E. A two-dimensional "flea on the elephant" phenomenon and its numerical visualization , Multiscale Model. Simul., Vol. 17, No. 1 (2019), pp. 137–166, DOI: 10.1137/18M1179985.…

GAMM19

Austria. 22.02.2019. From February 18th to 22nd, Azahar Monge, member of the DyCon project, participated in the 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM19)…

Greedy optimal control for elliptic problems and its application to turnpike problems

Hernández-Santamaría V., Lazar M., Zuazua E. Greedy optimal control for elliptic problems and itsapplication to turnpike problemsNUMER MATH. Vol. 141, No. 2, pp.455-493 (2019) DOI: 10.1007/s00211-018-1005-z Abstract: We adapt and…

On the convergence rate of the Dirichlet–Neumann iteration for unsteady thermal fluid–structure interaction

A. Monge, P. Birken On the convergence rate of the Dirichlet-Neumann iteration for unsteady thermal fluid-structure interaction. Comput Mech, Vol 62 (2018), pp. 525-541. DOI: 10.1007/s00466-017-1511-3 Abstract: We consider the…

Turnpike in optimal shape design for heat equation

G. Lance, E. Trélat, E. Zuazua Turnpike in optimal shape design for heat equation (2019) IFAC-PAPERSONLINE, Vol. 52, No. 16, pp. 496-501, DOI: 10.1137/17M1119160 Abstract: After a short presentation of…

Solving the Random Pielou Logistic Equation with the Random Variable Transformation Technique: Theory and Applications

J.-C. Cortés, A. Navarro-Quiles, J.-V. Romero, M.-D. Roselló Solving the Random Pielou Logistic Equation with the Random Variable Transformation Technique: Theory and Applications. MATH METHOD APPL SCI. Vol. 42, No.…

Mathematical model to asses impact of vih/aids infection in the spread of tuberculosis

Nkamba L. Mathematical model to assess vaccination and effective contact rate impact in the spread of tuberculosis (2019) Abstract: Tuberculosis is a serious problem of public health in several countries.…

Global Stability of a SVEIR Epidemic Model: Application to Poliomyelitis Transmission Dynamics

Nkamba L., Manga T., Ntaganda J. M., Abboubakar H., Kamgang J. C., Castelli L. Mathematical model to assess vaccination and effective contact rate impact in the spread of tuberculosis, Open…

Mathematical model to asses vaccination and effective contact rate in the spread of tuberculosis

Nkamba L., Manga T., Agouanet F., Manyombe M. Mathematical model to assess vaccination and effective contact rate impact in the spread of tuberculosis. J BIOL DYNAM. Vol. 13, No. 1…

Controllability of shadow reaction-diffusion systems

Hernández-Santamaría V., E. Zuazua. Controllability of shadow reaction-diffusion systems. J Differ Equations, Vol. 268, No. 7, pp. 3781-3818 (2020). DOI: 10.1016/j.jde.2019.10.012 Abstract: We study the null controllability of linear shadow…

Analysis of random non-autonomous logistic-type differential equations via the Karhunen-Loève expansion and the Random Variable Transformation technique

J.-C. Cortés, A. Navarro-Quiles, J.-V. Romero, M.-D. Roselló Analysis of random non-autonomous logistic-type differential equations via the Karhunen-Loève expansion and the Random Variable Transformation technique, COMMUN NONLINEAR SCI. Vol. 72…

Controllability and Positivity Constraints in Population Dynamics with Age Structuring and Diffusion

D. Maity, M. Tucsnak, E. Zuazua. Controllability and Positivity Constraints in Population Dynamics with Age Structuring and Diffusion, J MATH PURE APPL. Vol. 129 (2019), pp. 153-179. DOI: 10.1016/j.matpur.2018.12.006 Abstract:…

Decay rates for elastic-thermoelastic star-shaped networks

Han Z., Zuazua E. Decay rates for elastic-thermoelastic star-shaped networks Network and Heterogeneous Media, NETW HETEROG MEDIA, Vol. 12, No. 3 (2017), pp. 461-488. DOI: 10.3934/nhm.2017020 Abstract: This work discusses…

Controllability under positivity constraints of multi-d wave equations

Pighin, D., Zuazua, E. Controllability under positivity constraints of multi-d wave equations , Trends in Control Theory and Partial Differential Equations., Vol 32 (2019). DOI: 10.1007/978-3-030-17949-6_11 Abstract: We consider both…

Steady-state and periodic exponential turnpike property for optimal control problems in Hilbert spaces

Trélat E., Zhang C., and Zuazua E. Steady-state and periodic exponential turnpike property for optimal control problems in Hilbert spaces SIAM J. Control Optim., Vol. 2 (2018), pp. 1222-1252. DOI:…

Optimal shape design for 2D heat equations in large time

Trélat E., Zhang C., Zuazua E. Optimal shape design for 2D heat equations in large time J. Appl. Funct. Anal., Vol. 3 (2018), pp. 255-269. DOI: 1705.02764 Abstract: In this…

Minimal controllability time for finite-dimensional control systems under state constraints

Lohéac J., Trélat E., Zuazua, E. Minimal controllability time for finite-dimensional control systems under state constraints Automática, Vol. 96 (2018), pp. 380-392. DOI: 10.1016/j.automatica.2018.07.010 Abstract: We consider the controllability problem…

Corrigendum and addendum to “Hierarchic control for a coupled parabolic system”

Hernández-Santamaría V., de Teresa L., Poznyak A. Corrigendum and addendum to “Hierarchic control for a coupled parabolic system" . Portugaliae Math, Vol. 74, No. 2 (2017), pp.115-137. DOI: 10.4171/PM/1998 Abstract:…

Insensitizing controls for a semilinear parabolic equation: a numerical approach

Hernández-Santamaría V., de Teresa L., Boyer, F. Insensitizing controls for a semilinear parabolic equation: a numerical approach , MATH CONTROL RELAT F. AIMS. Vol. 9. No. 1 (2019), pp. 117-158, DOI:10.3934/mcrf.2019007…

Robust Stackelberg controllability for linear and semilinear heat equations

Hernández-Santamaría V., de Teresa L. Robust Stackelberg controllability for linear and semilinear heat equations. Evolution Equations & Control Theory AIMS, Vol.7, No. 2 (2018), pp.247-273, DOI:10.3934/eect.2018012 Abstract: In this paper…

Some remarks on the hierarchic control for coupled parabolic PDEs

Hernández-Santamaría V., de Teresa L. Some remarks on the hierarchic control for coupled parabolic PDEs . SEMA SIMAI Springer Series, Vol. 17 (2018), pp.117-137. DOI: 10.1007/978-3-319-97613-6_7 Abstract: In this paper,…

Internal Controllability for Parabolic Systems Involving Analytic Non-local Terms

Lissy P, and Zuazua E.Internal Controllability for Parabolic Systems Involving Analytic Non-local TermsCHINESE ANN MATH B. Vol. 39, No. 2 (2018), pp. 281-296 DOI: 10.1007/s11401-018-1064-6 Abstract: This paper deals with…

Boundary controllability for a one-dimensional heat equation with a singular inverse-square potential

U. Biccari Boundary controllability for a one-dimensional heat equation with a singular inverse-square potential, Math. Control Relat. F., Vol. 9, No. 1 (2019), pp. 191-219, DOI: 10.3934/mcrf.2019011 Abstract: We analyse…

The Poisson equation from non-local to local

U. Biccari, V. Hernández-Santamaría The Poisson equation from non-local to local, Electronic Journal of Differential Equations, Vol. 2018 (2018), No. 145, pp. 1-13. DOI: arXiv:1801.09470 Abstract: We analyze the limit…

Allee optimal control of a system in ecology

Trélat E., Zhu J., Zuazua, E. Allee optimal control of a system in ecology , Math. Models Methods Appl. Sci., Vol. 28, No. 09 (2018), pp. 1665-1697. DOI: 10.1142/S021820251840002X Abstract:…

Preface: A tribute to professor Eduardo Casas on his 60th birthday

Fernández L.A., Mateos M., Pola C., Tröltzsch F., Zuazua E. Preface: A tribute to professor Eduardo Casas on his 60th birthday MATH CONTROL RELAT F. Vol. 8, No. 1 (2018)…

Optimal control of the Lotka–Volterra system: turnpike property and numerical simulations

Ibañez A. Optimal control of the Lotka–Volterra system: turnpike property and numerical simulations J. Biol. Dyn., Vol. 11, No. 1 (2016), pp.25-41, DOI: 10.1080/17513758.2016.1226435 Abstract: The Lotka–Volterra model is a…

Controllability under positivity constraints of semilinear heat equations

Pighin, D., Zuazua, E. Controllability under positivity constraints of semilinear heat equations MATH CONTROL RELAT F., Vol. 8, No. 3-4 (2018). DOI: 10.3934/mcrf.2018041 Abstract: In many practical applications of control…

Hierarchic control for a coupled parabolic system

Hernández-Santamaría V., de Teresa L., Poznyak A. Hierarchic control for a coupled parabolic system . Port. Math. Vol. 73 (2016), pp. 115-137, DOI: 10.4171/PM/1979 Abstract: In this paper we study…

Controllability of a one-dimensional fractional heat equation: theoretical and numerical aspects

U. Biccari, V. Hernández-Santamaría Controllability of a one-dimensional fractional heat equation: theoretical and numerical aspects, IMA J. Math. Control Inf., Vol. 36, No. 4 (2019), pp. 1199-1235. DOI: 10.1093/imamci/dny025 Abstract:…

Local regularity for fractional heat equations

U. Biccari, M. Warma, E. Zuazua Local regularity for fractional heat equations<, Recent Advances in PDEs: Analysis, Numerics and Control, SEMA SIMAI Springer Series, Vol. 17 (2018). DOI: 10.1007/978-3-319-97613-6 Abstract:…

Controllability of Evolution Equations with Memory

Felipe W. Chaves-Silva, Xu Zhang, and Enrique Zuazua Controllability of Evolution Equations with Memory. SIAM J. Control Optim., 55(4), 2437–2459. (23 pages) DOI: 10.1137/151004239 Abstract: This article is devoted to studying…

Null controllability for wave equations with memory

Lu Q., Zhang X., Zuazua E. Null controllability for wave equations with memory, J. Math. Pures Appl., Vol. 108, No. 4 (2017), pp. 500-531. DOI: 10.1016/j.matpur.2017.05.001 Abstract: We study the…

Filtered gradient algorithms for inverse design problems of one-dimensional Burgers equation

L. Gosse, E. Zuazua. Filtered gradient algorithms for inverse design problems of one-dimensional Burgers equation. Innovative Algorithms and Analysis,Gosse, Laurent, Natalini, Roberto (Eds.), Springer INdAM Series 16, 2017, 197-228. DOI:…

Averaged controllability of parameter dependent conservative semigroups

Lohéac J., Zuazua E. Averaged controllability of parameter dependent conservative semigroups Journal of Differential Equations, 262 (3) (2017), 1540–1574 DOI: 10.1016/j.jde.2016.10.017 Abstract: We consider the problem of averaged controllability for…

Minimal controllability time for the heat equation under unilateral state or control constraints

Lohéac J., Trélat E., Zuazua E. Minimal controllability time for the heat equation under unilateral state or control constraints . Mathematical Models and Methods in Applied Sciences, Volume 27, Issue 09,…

Local elliptic regularity for the Dirichlet fractional Laplacian

U. Biccari, M. Warma, E. Zuazua Local elliptic regularity for the Dirichlet fractional Laplacian Advanced Nonlinear Studies, Vol. 17, Nr. 2 (2017), pp. 387-409. DOI: 10.1515/ans-2017-0014 Abstract: We analyze the…

Addendum: Local elliptic regularity for the Dirichlet fractional Laplacian

U. Biccari, M. Warma, E. Zuazua Addendum: Local elliptic regularity for the Dirichlet fractional Laplacian Adv. Nonlinear Stud., Vol. 17, Nr. 4 (2017), pp. 837-839. DOI: 10.1515/ans-2017-6020 Abstract: In [1],…

Large time control and turnpike properties for wave equations

Zuazua E. Large time control and turnpike properties for wave equations ANNU REV CONTROL. Vol. 40 (2017), pp. 199-210 DOI: 10.1016/j.arcontrol.2017.04.002 Abstract: In the last decades mathematical control theory has…

Actuator design for parabolic distributed parameter systems with the moment method

Privat Y., Trélat E., Zuazua E. Actuator design for parabolic distributed parameter systems with the moment method SIAM J CONTROL OPTIM. Vol. 55, No. 2 (2017), pp. 1128–1152. DOI: 10.1137/16M1058418…

Optimal observability of the multi-dimensional wave and Schrödinger equations in quantum ergodic domains

Privat Y., Trélat E., Zuazua E. Optimal observability of the multi-dimensional wave and Schrödinger equations in quantum ergodic domains J EUR MATH SOC. Vol. 18, No. 5 (2016), pp. 1043–1111…

Dispersion for 1-D Schrödinger and wave equations with BV coefficients

Beli C. N., Ignat L. I., Zuazua E. Dispersion for 1-D Schrödinger and wave equations with BV coefficients ANN I H POINCARE-AN. Vol. No. 33 (2016), pp. 1473-1495. DOI: 10.1016/j.anihpc.2015.06.002…

Numerical aspects of sonic-boom minimization

Allahverdi N., Pozo A., Zuazua E. Numerical aspects of sonic-boom minimization COMMUN CONTEMP MATH. Vol. No. 658 (2016), pp. 267 - 279. DOI: 10.1090/conm/658/13133 Abstract: The propagation of the sonic-boom…

Numerical meshes ensuring uniform observability of one-dimensional waves: construction and analysis

Ervedoza S., Marica A., Zuazua E. Numerical meshes ensuring uniform observability of one-dimensional waves: construction and analysis IMA J NUMER ANAL. Vol. 36, No. 2 (2016), pp. 503–542. DOI: 10.1093/imanum/drv026…

Averaged controllability for random evolution Partial Differential Equations

Lu Q., Zuazua E. Averaged controllability for random evolution Partial Differential Equations J MATH PURE APPL. Vol. 105, No. 3 (2016)., pp. 367–414. DOI: 10.1016/j.matpur.2015.11.004 Abstract: We analyze the averaged…

Numerical aspects of large-time optimal control of Burgers equation

Allahverdi N., Pozo A., Zuazua E. Numerical aspects of large-time optimal control of Burgers equation ESAIM-MATH MODEL NUM. Vol. 50. No. 5 (2016). DOI: 10.1051/m2an/2015076 Abstract: In this paper, we…

Remarks on Long Time Versus Steady State Optimal Control

Porretta A., Zuazua E. Remarks on Long Time Versus Steady State Optimal Control Mathematical Paradigms of Climate Science -Springer INdAM Series, Vol. 15 (2016), pp 67-89, DOI: 10.1007/978-3-319-39092-5_5 Abstract: Control…

Exact penalization of terminal constraints for optimal control problems

Gugat M., Zuazua E. Exact penalization of terminal constraints for optimal control problems >OPTIM CONTR APPL MET., Vol. 37, No. 6 (2016), pp. 1329–1354, DOI: 10.1002/oca.2238 Abstract: We study optimal…

Randomised observation, control and stabilization of waves

Privat Y., Trélat E., Zuazua E. Randomised observation, control and stabilization of waves J Appl Math Mech Z Angew Math Mech. Vol. 96, No. 5 (2016), pp. 538-549, DOI: 10.1002/zamm.201500181…

On the lack of controllability of fractional in time ODE and PDE

Lu Q., Zuazua E. On the lack of controllability of fractional in time ODE and PDE MATH CONTROL SIGNAL. Vol. No. 2 (2016), pp. 28:10 ,DOI: 10.1007/s00498-016-0162-9 Abstract: This paper…

Optimal Neumann control for the 1D wave equation

Gugat M., Trélat E., Zuazua E. Optimal Neumann control for the 1D wave equation: Finite horizon, infinite horizon, boundary tracking terms and the turnpike property SYST CONTROL LETT. Vol. No.…

Optimal strategies for driving a mobile agent in a “guidance by repulsion” model

Escobedo R., Ibañez A., Zuazua E Optimal strategies for driving a mobile agent in a “guidance by repulsion” model COMMUN NONLINEAR SCI., Vol.39 (2016), pp. 58-72, DOI: 10.1016/j.cnsns.2016.02.017 Abstract: We…

Stable observation of additive superpositions of Partial Differential Equations

E. Zuazua. Stable observation of additive superpositions of Partial Differential Equations. Syst. Control. Lett. Vol.93 (2016), pp. 21–29, DOI: 10.1016/j.sysconle.2016.02.017 Abstract: We address the problem of observing the solutions of a…

From averaged to simultaneous controllability

Lohéac J., Zuazua E. From averaged to simultaneous controllability Ann. Fac. Sci. Toulouse Math. Vol.25, No.4 (2016), pp. 785-828, DOI: 10.5802/afst.1511 Abstract: We consider a linear finite dimensional control system…

Null Controllability of Linear Heat and Wave Equations with Nonlocal Spatial Terms

Fernández-Cara E., Lu Q., Zuazua E. Null Controllability of Linear Heat and Wave Equations with Nonlocal Spatial Terms SIAM J. Control Optim. Vol. 54, No.4 (2019) DOI: 10.1137/15M1044291 Abstract: In…

Null controllability for a heat equation with a singular inverse-square potential involving the distance to the boundary function

U. Biccari, E. Zuazua Null controllability for a heat equation with a singular inverse-square potential involving the distance to the boundary function J. Differential Equations, Vol. 261, No. 5 (2016),…

Decay rates for 1−d heat-wave planar networks

Han Z.-J., Zuazua E. Decay rates for 1−d heat-wave planar networks NETW HETEROG MEDIA. Vol. 11, No. 4 (2016), pp. 655–692,DOI: 10.3934/nhm.2016013 Abstract: The large time decay rates of a…

Greedy controllability of finite dimensional linear systems

Lazar M., Zuazua E. Greedy controllability of finite dimensional linear systems Automatica, Vol.74 (2016), pp. 327-340 DOI: 10.1016/j.automatica.2016.08.010 Abstract: We analyse the problem of controllability for parameter-dependent linear finite-dimensional systems.…

Norm saturating property of time optimal controls for wave-type equations

Lohéac. J, Zuazua E. Norm saturating property of time optimal controls for wave-type equations IFAC-PapersOnLine, Vol. 49, No.8 (2016), pp. 37-42. DOI: 10.1016/j.ifacol.2016.07.415 Abstract: We consider a time optimal control…

Lipschitz dependence of the coefficients on the resolvent and greedy approximation for scalar elliptic problems

We analyze the inverse problem of identifying the diffusivity coefficient of a scalar elliptic equation as a function of the resolvent operator. We prove that, within the class of measurable coefficients, bounded above and below by positive constants, the resolvent determines the diffusivity in an unique manner...

Numerical hypocoercivity for the Kolmogorov equation

We prove that a finite-difference centered approximation for the Kolmogorov equation in the whole space preserves the decay properties of continuous solutions as $ t \to \infty $, independently of the mesh-size parameters.