Darlis Bracho Tudares – Page 2

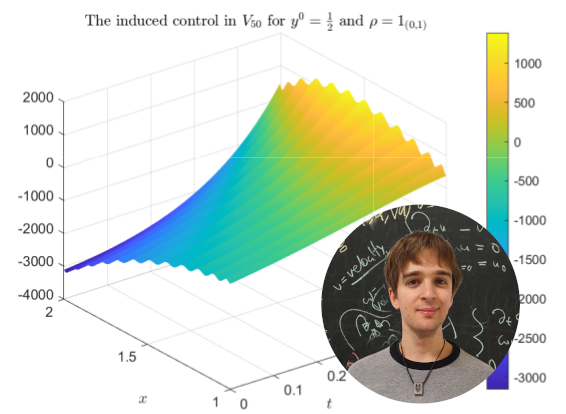
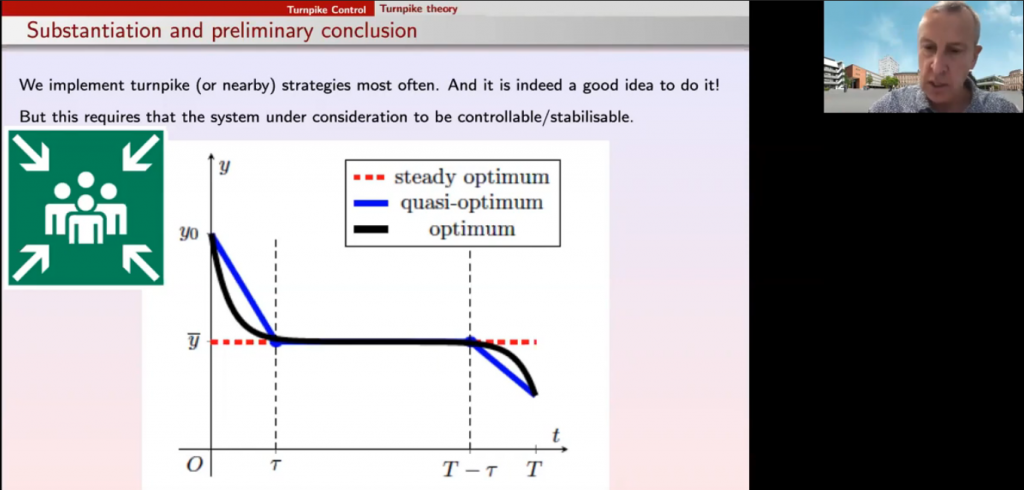
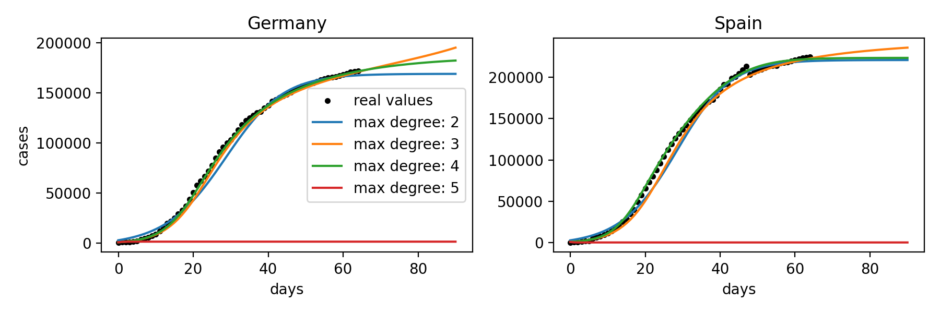
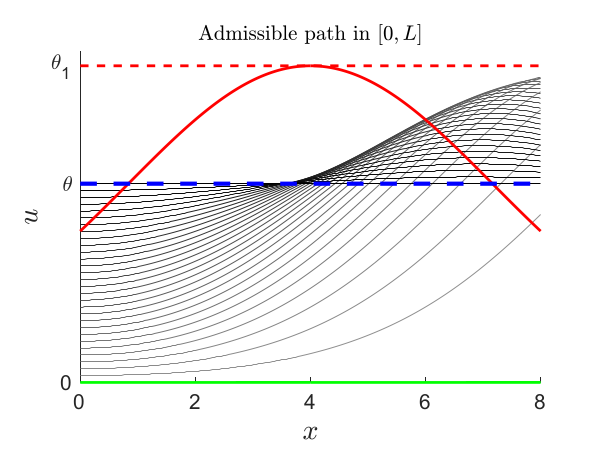
Multilevel control by duality

Umberto Biccari, Enrique Zuazua. Multilevel control by duality (2023) Systems & Control Letters, Vol. 175, 105-502, https://doi.org/10.1016/j.sysconle.2023.105502 Abstract. We discuss the multilevel control problem for linear dynamical systems, consisting in designing…

FBP2021 | Inverse design for Conservation laws and Hamilton-Jacobi equations by E. Zuazua

On Friday September 17, our Head Enrique Zuazua will give a plenary talk on "Inverse design for Conservation laws and Hamilton-Jacobi equations" on the FBP conference (online), from September 13th.…

Model predictive control with random batch methods for a guiding problem

Agent-based models, Guiding problem, large scale complex systems, Random

Ko Dongnam, Zuazua Enrique. Model predictive control with random batch methods for a guiding problem (2021). Math. Models Methods Appl. Sci., Vol. 31, No. 8, pp. 1569-1592. (2021) DOI: https://doi.org/10.1142/S0218202521500329…

SHU Course: Principles of AI for Control and Optimization

From this month, September 07th. to November 11th., the Shanghai University (China) is hosting the short course on "Principles of AI for Control and Optimization" by: -Our Head Enrique Zuazua…

Classical system theory revisited for Turnpike in standard state space systems and impulse controllable descriptor systems

descriptor systems, linear systems, long time behavior, optimal control, Riccati equations

Heiland J., Zuazua E. Classical system theory revisited for Turnpike in standard state space systems and impulse controllable descriptor systems (2021) SIAM J. Control Optim., Vol. 59.5 (2021), pp. 3600-3624 Abstract.…

Course on Spherical Geometry by Elisa Affili

This summer, on August 30-31, 2021 our Postdoctoral Researcher Elisa Affili gave a course on "Spherical Geometry" at the 3rd edition of the Summer STEM Academy 2021, the summer school…

Summer course (China): Control, Machine Learning and Numerics by E. Zuazua

On July 09th. to July 26th., our Head Enrique Zuazua gave a course on "Control, Machine Learning and Numerics" organized by Tianyuan Mathematical Center in Northeast China and Jilin University…

Optimal control for neural ODE in a long time horizon and applications to the classification and simultaneous controllability problems

Jon Asier Bárcena-Petisco. Optimal control for neural ODE in a long time horizon and applications to the classification (2021) Abstract. We study the optimal control in a long time horizon…

33rd. CBM – Brazilian Colloquium of Mathematics

Next month, on August 5th., our Postdoctoral Researcher Elisa Affili will talk on "A mathematical model for civil wars: a new Lotka-Volterra competitive system" at the 33rd. CBM - The…

The turnpike property in nonlinear optimal control – A geometric approach

Nonlinear system, optimal control, Turnpike

N. Sakamoto, E. Zuazua. The turnpike property in nonlinear optimal control - A geometric approach. (2021) Automatica., Vol. 134 (2021), p. 109939 Abstract: This paper presents, using dynamical system theory,…

ERC researchers encounter at UAM

Last month, on June 25th our Head Enrique Zuazua, talked about at the special event organized by Prof. José Luis Pau from the Department of Science at UAM - Autonomous…

Summer short course (China): Control, Machine Learning and Numerics by E. Zuazua

This month, on July 09th. to July 26th., our Head Enrique Zuazua will give a course on "Summer short course (China): Control, Machine Learning and Numerics" organized by Tianyuan Mathematical…

Control of reaction-diffusion equation with state constraints -INdAM Workshop

Next Wednesday on July 7th., our team member Domènec Ruiz-Balet from UAM will talk about "Control of reaction-diffusion equation with state constraints” at the INdAM Workshop on Analysis and Numerics…

A quantitative analysis of Koopman operator methods for system identification and predictions

C. Zhang, E. Zuazua. A quantitative analysis of Koopman operator methods for system identification and predictions (2023) Comptes Rendus. Mécanique, Vol. 351, No. S1, pp. 1-31. In memory of R.…

Optimal control of linear non-local parabolic problems with an integral kernel

Umberto Biccari, Víctor Hernández-Santamaría, Loic Louison, Abdennebi Omrane. Optimal control of linear non-local parabolic problems with an integral kernel. (2021) Abstract. We consider a linear non-local heat equation in a bounded…

Blow-up results for a logarithmic pseudo-parabolic p(.)-Laplacian type equation

Abita Rahmoune, Umberto Biccari. Blow-up results for a logarithmic pseudo-parabolic -Laplacian equation. (2021) Abstract. In this paper, we consider an initial-boundary value problem for the following mixed pseudo-parabolic p(.)-Laplacian type equation…

Multilevel Selective Harmonic Modulation via Optimal Control -INdAM workshop

This month on July 2nd., our team member Umberto Biccari will talk about "Multilevel Selective Harmonic Modulation via Optimal Control" at the INdAM Workshop on Analysis and Numerics of Design,…

Jon Asier Bárcena-Petisco: Premio de Investigación Matemática Vicent Caselles 2021

Spain. 29.06.2021. The Chair of Computational Mathematics at University of Deusto is glad to announce our Postdoctoral Researcher Jon Asier Bárcena-Petisco has been awarded "Premio de Investigación Matemática Vicent Caselles…

ERC DyCon Postdoctoral open position 2021-2022

This call is CLOSED! The Chair of Computational Mathematics at Fundación Deusto in Bilbao, Basque Country - Spain, led by Prof. Dr. Enrique Zuazua, is looking for candidates to fill…

INdNAM workshop: “Analysis and Numerics of Design, Control and Inverse Problems”

The next INdNAM workshop: “Analysis and Numerics of Design, Control and Inverse Problems” organized by the Scientific Committee by Giuseppe Floridia (Università Mediterranea di Reggio Calabria) in Rome, Italy and Enrique Zuazua (Head of the Chair fur…

OCA’21 Online CIMPA School

On June 28th. to July 3rd., our Head Enrique Zuazua will talk on "Control, Numerics and Machine Learning" at the Online CIMPA School (OCA'21): Optimal Control and its Applications in…

Borjan Geshkovski -PhD Thesis defense: “Control in Moving Interfaces and Deep Learning”

Last month, on May 14th, our team member Borjan Geshkovski at CCM - Chair of Computational Mathematics, Deusto Foundation - University of Deusto, defended his PhD Thesis on: Control in…

Local null controllability of the penalized Boussinesq system with a reduced number of controls

J.A. Bárcena-Petisco, Kevin Le Balc'H. Local null controllability of the penalized Boussinesq system with a reduced number of controls (2021) Abstract. In this paper we consider the Boussinesq system with homogeneous…

Enrique Zuazua: TOP TALENT de la CIENCIA

Date: Wed. May 26, 2021 Organized by: Deia - Noticias de Bizkaia (Basque Country Media) Title: Deia Top Talent Sariak 2021 - Enrique Zuazua: TOP TALENT CIENCIA Laureate: Prof. Dr.…

Networks, Waves and Control

On Wednesday June 9, our Head Enrique Zuazua will talk about "Networks, Waves and Control", an Analysis Seminar of the Department "R. Caccioppoli" at Università degli studi di Napoli Federico…

Initial data identification for the one-dimensional Burgers equation

Thibault Liard, Enrique Zuazua. Initial data identification for the one-dimensional Burgers equation. (2022). IEEE T Automat. Contr., Vol. 67, No. 6, pp. 3098-3104, DOI: 10.1109/TAC.2021.3096921 Abstract. In this paper, we…

Control of Hyperbolic and Parabolic Equations on Networks and Singular limits

advection-diffusion equations, Controllability, cost of controllability, network, singular limits, vanishing viscosity

J.A. Bárcena-Petisco, M. Cavalcante, G.M. Coclite, N. de Nitti, Enrique Zuazua. Control of Hyperbolic and Parabolic Equations on Networks and Singular limits (2021) Abstract. We study the controllability properties of the…

StudOn AG Neural Differential Equations, Control and Machine Learning

On May 11th, our Head Enrique Zuazua talked about "Neural Differential Equations, Control and Machine Learning" at StudOn AG "Mathematics and Deep Learning". Abstract. We discuss Neural Ordinary Differential Equations…

The turnpike property in semilinear control

D. Pighin The turnpike property in semilinear control ESAIM Control Optim. Calc. Var., Vol. 26 (2021), pp. 1-48 Abstract.An exponential turnpike property for a semilinear control problem is proved. The…

Neural Differential Equations, Control and Machine Learning

Next Monday April 26, our Head Enrique Zuazua will be talking about "Neural Differential Equations, Control and Machine Learning" on the webinar by DSAD - Data Science Across Disciplines, a…

CCM double-seminar: Research Topics: control questions in Lotka-Volterra and cross-diffusion models and Generative modelling and normalizing flows

On April 19th, our team members at CCMDeusto, Elisa Affili Postdoctoral Researcher and Pierre Mordant with an Internship from Ecole Polytechnique, will be talking in a double session as part…

Chaire Jean-Morlet 2021: Dynamics and Control of a guiding Model by E. Zuazua

On March 22nd, our Head Enrique Zuazua gave a talk about "Dynamics and Control of a guiding Model" at Kinetic Equations: from Modeling, Computation to Analysis an event from the …

DyCon blog: Multilevel Selective Harmonic Modulation via Optimal Control

Spain. 12.04.2021. Our team members Deyviss Jesús Oroya-Villalta, Carlos Esteve-Yagüe and Umberto Biccari, made a contribution to the DyCon Blog about "Multilevel Selective Harmonic Modulation via Optimal Control": Selective harmonic Modulation (SHM)…

Jornada de Primavera en EDPs

Next Friday April 9, our postdoctoral researchers Carlos Esteve Yagüe and Jon Asier Bárcena Petisco will be talking at the "Jornada de Primavera en EDPs" (Spring day in EDPs) organized…

The Finite-Time Turnpike Phenomenon for Optimal Control Problems: Stabilization by Non-smooth Tracking Terms

M. Gugat, M. Schuster, E. Zuazua. The Finite-Time Turnpike Phenomenon for Optimal Control Problems: Stabilization by Non-Smooth Tracking Terms, in "Stabilization of Distributed Parameter Systems: Design Methods and Applications". Grigory…

Large-time asymptotics in deep learning

deep learning, Neural ODEs, optimal control, Residual Neural Networks, Supervised Learning, turnpike property

Esteve C., Geshkovski B., Pighin D., Zuazua E. Large-time asymptotics in deep learning (2021). hal-02912516 Abstract. It is by now well-known that practical deep supervised learning may roughly be cast as…

Multiplicity of solutions for fractional q(.)-Laplacian equations

Abita Rahmoune, Umberto Biccari. Multiplicity of solutions for fractional -Laplacian equations. (2021) Abstract. In this paper, we deal with the following elliptic type problem where is a measurable function and is…

Multilevel Selective Harmonic Modulation via Optimal Control

Umberto Biccari, Carlos Esteve-Yagüe, Deyviss Jesús Oroya-Villalta. Multilevel Selective Harmonic Modulation via Optimal Control. (2022) Applied Mathematics and Optimization Abstract. We consider the Selective Harmonic Modulation (SHM) problem, consisting in the…

Cafés Scientifique de la Culture: Engagez-moi, je suis mathématicien, by E. Zuazua

On Thursday March 25, our Head Enrique Zuazua gave the talk "Hire me, I'm a Mathematician"" at Cafés Scientifique de la Culture an online event organized by the French-speaking Pole at…

Local null controllability of a model system for strong interaction between internal solitary waves

Jon Asier Bárcena-Petisco, Sergio Guerrero and Ademir F. Pazoto. Local null controllability of a model system for strong interaction between internal solitary waves. Commun. Contemp. Math. (2021) https://doi.org/10.1142/S0219199721500036 Abstract. In…

DyCon blog: Points of Interest Extraction and Prediction of Next Locations

Spain. 10.03.2021. Aicha Karite recent member from our team, made a contribution to the DyCon Blog about "Points of Interest Extraction and Prediction of Next Locations": Generally, a prediction problem…

Control and Deep Learning: Some connections

B. Geshkovski, E. Zuazua. Control and Deep Learning: Some connections (2021) This note is an extended abstract for a talk given by the second author during the workshop ”Challenges in…

Perceptrons, Neural Networks and Dynamical Systems

Spain. 09.03.2021 Author: Sergi Andreu Perceptrons, Neural Networks and Dynamical Systems // This post is last part of the "Deep Learning and Paradigms" post Binary classification with Neural Networks When dealing with data classification,…

Deep Learning & Paradigms

Spain. 01.03.2021 Author: Sergi Andreu Deep Learning & Paradigms By

Open World PDE Seminar: Inverse design for conservation laws and Hamilton–Jacobi equations

Last Tuesday February 2nd, our Head Enrique Zuazua talked at One World PDE event about: Inverse design for conservation laws and Hamilton–Jacobi equations Abstract. We shall discuss the inverse problem,…

Opening the black box of Deep Learning

Spain. 24.02.2021 Author: Sergi Andreu Opening the black box of Deep Learning By

Coloquio MTM UFSC: Inverse design for conservation laws and Hamilton-Jacobi equations by E. Zuazua

Next Friday March 5th, our Head Enrique Zuazua will talk about “Inverse design for conservation laws and Hamilton-Jacobi equations”, a lecture on the Colloquium organized by the Department of Mathematics…

Research at service of Society

Last year the pandemic has been crucial on our lives. From University of Deusto, we can proudly say all our people, specially research staff have quickly adapted to the new…

Nonnegative control of finite-dimensional linear systems

Dirac impulse, Minimal time, Nonnegative control

Lohéac J., Trélat E., Zuazua E. Nonnegative control of finite-dimensional linear systems. Ann. I. H. Poincare-An., Vol. 38, No. 2, pp. 301-346. (2021) DOI: https://doi.org/10.1016/j.anihpc.2020.07.004 Abstract. We consider the controllability…

Reachable subspaces, control regions and heat equations with memory

control regions, Controlled heat equations with memory, reachable subspaces

G. Wang, Y. Zhang, E. Zuazua. Reachable subspaces, control regions and heat equations with memory. (2021) Abstract. We study the controlled heat equations with analytic memory from two perspectives: reachable…

ERC DyCon Postdoctoral position

The Chair of Computational Mathematics of Fundación Deusto in Bilbao, Basque Country - Spain, led by Prof. Dr. Enrique Zuazua, is looking for candidates to fill postdocs positions at the…

CCM – How we did it on 2020!

Spain. 31.12. 2020. In a very challenging year, the Chair of Computational Mathematics of Fundación Deusto at University of Deusto (Bilbao, Basque Country - Spain) shared this infographics to show…

Analysis and numerics solvability of backward-forward conservation laws

Backward-forward method, Conservation Laws, Identification problems, Non-smooth optimization problem, Wave-front tracking algorithm, Weak-entropy solutions

Thibault Liard, Enrique Zuazua. Analysis and numerics solvability of backward-forward conservation laws. (2020) Abstract. In this paper, we study the problem of initial data identification for the one-dimensional Burgers equation.…

Turnpike Control and Deep Learning by Enrique Zuazua

Worldwide. On December 10th. our Head Enrique Zuazua talked about “Turnpike control and deep learning”, a seminar organized by the MOX Politecnico di Milano. The turnpike principle, ubiquitous in applications,…

The interplay of Deep Learning and Control Theory by Borjan Geshkovski

On December 09th our team member Borjan Geshkovski PhD student at DyCon ERC Project from UAM, will give a talk at "AG Mathematics of Deep Learning" by Friedrich-Alexander Universität Erlangen-Nürnberg…

DyCon blog: Averaged dynamics and control for heat equations with random diffusion

Spain. 04.12.2020. Our team member Jon Asier Bárcena Petisco and our Head Enrique Zuazua made a contribution to the DyCon Blog about "Averaged dynamics and control for heat equations with…

Inverse design for conservation Laws and Hamilton-Jacobi equations

Next saturday December 05th. our Head Enrique Zuazua will be talking about Inverse design for conservation Laws and Hamilton-Jacobi equations organized by the School of Mathematical Sciences of the North…

3rd BYMAT Session by Jon Asier Bárcena Petisco

bymat, Controllability, heat equation, Lipschitz

Today December 3rd our Postdoctoral member Jon Asier Bárcena Petisco talked about "Some recent results about the controllability of the heat equation" at the event 3rd. BYMAT - Bringing Young Mathematicians…

PhD and Postdoc positions in Applied Mathematics at FAU

The Chair in Applied Analysis - Alexander von Humboldt Professorship led by Enrique Zuazua at FAU Erlangen-Nürnberg is looking for outstanding candidates to fill several PhD and Postdoctoral positions: Focused…

HKSIAM Seminar by E. Zuazua: Turnpike control and deep learning

deep learning, DL, Turnpike

Worldwide. This wednesday November 25th. our Head Enrique Zuazua will be talking about "Turnpike control and deep learning" in the Applied Mathematics Seminars for HKSIAM and Hong Kong Universities organized…

The Inverse Problem for Hamilton-Jacobi equations and Semiconcave Envelopes

Hamilton-Jacobi equation, inverse design problem, obstacle problems, semiconcave envelopes

Esteve C., Zuazua E.. The Inverse Problem for Hamilton-Jacobi equations and Semiconcave Envelopes SIAM J. Math. Anal., Vol. 52, No. 6, pp. 5627–5657 (2020). https://doi.org/10.1137/20M1330130 Abstract. We study the inverse…

The Fields Institute 2nd Symposium on Machine Learning and Dynamical Systems

Worldwide. 12.11.2020. The Fields Institute for Research in Mathematical Sciences (Toronto, Canada) organized the 2nd Symposium on Machine Learning and Dynamical Systems, a virtual event organized with researchers all around…

Averaged dynamics and control for heat equations with random diffusion by Jon Asier Bárcena Petisco

Yesterday November 10th, our Postdoctoral researcher Jon Asier Bárcena Petisco gave a talk in the "Control in Times of Crisis" Seminar about: "Averaged dynamics and control for heat equations with…

Hire me! I’m a Mathematician – by Enrique Zuazua

This Friday November 6th our Head Enrique Zuazua will be giving the workshop “Hire me, I’m a Mathematician“ at the "XX Semana de la Ciencia" (20th Science Week) organized by…

DyCon blog: Q-learning for finite-dimensional problems

Spain. 29.10.2020. Our team member Carlos Esteve made a contribution to the DyCon Blog about "Q-learning for finite-dimensional problems": Reinforcement Learning (RL) is, together with Supervised Learning and Unsupervised Learning,…

XX Semana de la Ciencia

On November 3, 4, 6, 10 and 12 the Department of Mathematics of the UAM - Universidad Autónoma de Madrid organized the "XX Semana de la Ciencia" (20th. Week of…

Large-time asymptotics in Deep Learning by Borjan Geshkovski

deep learning

Last Friday October 23rd our team member Borjan Geshkovski PhD student at DyCon ERC Project from UAM, gave a talk at "Seminario de estadística" organized by the UAM - Universidad…

PhD for Mathematical Modelling, Simulation and Optimization Using the Example of Gas Networks at TRR 154

Open position for a doctoral candidate at FAU Erlangen-Nürnberg to work on the dynamics, control and of partial differential equations motivated by gas network dynamics. The main aim of TRR…

CCM Seminar: Averaged dynamics and control for heat equations with random diffusion

Spain. 23.10.2020. Last Tuesday on October 20th, 2020, our team member Jon Asier Bárcena Petisco Postdoctoral researcher from UAM will be talking about "Averaged dynamics and control for heat equations…

Control under constraints for multi-dimensional reaction-diffusion monostable and bistable equations

Constraints, Controllability, Mathematical biology, Reaction-diffusion

Ruiz-Balet D., Zuazua E.. Control under constraints for multi-dimensional reaction-diffusion monostable and bistable equations. J. Math. Pures Appl, vol. 143, pp. 345-375 (2020) https://doi.org/10.1016/j.matpur.2020.08.006 Abstract. Dynamic phenomena in social and…

Moving control strategy for memory-type equations

Spain. 20.10.2020. Jesus Oroya and Umberto Biccari, researchers at our team, made a contribution to the DyCon Blog about "Moving control strategy for memory-type equations" Take a look the detailed…

Optimal Control and Design of Structures and Fluids by Enrique Zuazua

Worldwide. 02.10.2020. Yesterday October 1st. our Head Enrique Zuazua presented "Control y Diseño Óptimo de Estructuras y Fluidos" (Optimal Control and Design of Structures and Fluids) invited by the Department…

Enrique Zuazua – Seminar on PDE and Applied Mathematics, Brazil

Worldwide. 29.09.2020. Last Wednesday September 23rd. the UFF - Fluminense Federal University (Universidade Federal Fluminense) and the UFRJ - University of Brazil (Federal University of Rio de Janeiro) from Rio…

Turnpike Control and Deep Learning by Enrique Zuazua at IITK

deep learning, Neural ODEs, optimal control, Residual Neural Networks, Supervised Learning, turnpike property

Worldwide. 08.09.2020. Yesterday, our Head Enrique Zuazua gave a talk about "Turnpike Control and Deep Learning" hosted by IITK - Indian Institute of Technology, Kampur in collaboration with IISER-Kolkata, IISER-Pune,…

An Introduction to Reinforcement Learning and Optimal Control Theory

DS, dynamical systems, HJB equation, MDP, Reinforcement Learning, RL

Organized by CCM - Chair of Computational Mathematics Speaker: Carlos Esteve Yague, Postdoctoral Researcher at CCM From September 8th. to October 1st, 2020 Sessions: 4, one session/week Abstract. This mini-course…

Turnpike Control and Deep Learning – Fields Institute 2nd Simposium on Machine Learning and Dynamical Systems

deep learning, Neural ODEs, optimal control, Residual Neural Networks, Supervised Learning, turnpike property

Worldwide. 01.09.2020. The Fields Institute for Research in Mathematical Sciences at the University of Toronto, Canada organized the Second Simposium on Machine Learning and Dynamical Systems on September 21st to…

CMAI Colloquium Fall 2020 – 1st session by Enrique Zuazua

Worldwide. 28.08.2020. Last friday August 28th, 2020 our Head Enrique Zuazua gave the first lecture of the Center for Mathematics and Artificial Intelligence (CMAI) Colloquium this fall about "Turnpike Control…

Tips for a good SyG interview

Worldwide. 29.07.2020. Last Tuesday July 21st, 2020, Enrique Zuazua Head of CCM - Chair of Computational Mathematics gave a talk about: "Tips for a good SyG interview"a session organized to…

The turnpike with lack of observability

Pighin D., Sakamoto N. The turnpike with lack of observability (2020) Abstract: We obtain turnpike results for optimal control problems with lack of stabilizability in the state equation and/or detectability in…

Gender Roles in Maths

Worldwide. 02.07.2020. Science, Technology, Engineering and Mathematics (STEM) fields are usually associated with boys but what about girls achievements? Are there real differences between them? A lot of research and…

Less health and money, and more heartbreak

Worldwide. 02.07.2020. In a world still living the hard shake of COVID-19, our Head Enrique Zuazua put on the table on an article published on the basque journal Deia (Spanish)…

Shape turnpike for linear parabolic PDE models

Direct methods, Optimal shape design, Parabolic equation, Strict dissipativity, Turnpike

Lance G., Trélat E., Zuazua E. Shape turnpike for linear parabolic PDE models Syst. Control. Lett. Vol. 142 (2020). DOI: 10.1016/j.sysconle.2020.104733 Abstract: We introduce and study the turnpike property for…

A stochastic approach to the synchronization of coupled oscillators

coupled oscillators, gradient descent, Kuramoto model, optimal control, random batch method, synchronization

Umberto Biccari, Enrique Zuazua. A stochastic approach to the synchronization of coupled oscillators. Frontiers in Energy Research, section Smart Grids. Front. Energy Res. Vol. 8 (2020). DOI: 10.3389/fenrg.2020.00115 Abstract. This paper…

At FAU-ZISC “Data-Driven COVID Modeling”

Worlwide. 10.06.2020. During COVID-19 the World recognized the important role of Mathematics when critical decisions has to be made using the information and data analysis from mathematical models for the…

Dynamics, Numerics and Control of Reaction-Diffusion Models Arising in Social and Biological Sciences

Worldwide. 05.06.2020. On May 29th our Head Enrique Zuazua gave a lecture invited by the Shanghai Jiao Tong University about "Dynamics, Numerics and Control of Reaction-Diffusion Models Arising in Social…

New Approaches to controlling Dynamics

Worlwide (ERC site). In 2018 the ERC - European Research Council published on its website an entry about the DyCon Project led by our Head Enrique Zuazua where the team…

Full probabilistic solution of a infinite dimensional linear control system with random initial and final conditions

finite dimensional, linear control system, probabilistic

J.-C. Cortes, A. Navarro-Quiles, J.-V. Romero, M.-D. Rosello, E. Zuazua. Full probabilistic solution of a infinite dimensional linear control system with random initial and final conditions. J. Franklin I. (2020)…

Synchronized Oscillators

Spain. 03.06.2020. Umberto Biccari, and Enrique Zuazua made a contribution to the DyCon Blog about " Synchronized Oscillators" Take a look the detailed explanation at DyCon Blog All posts at…

Stochastic optimization for simultaneous control

Spain. 03.06.2020. Ana Navarro, Umberto Biccari, and Enrique Zuazua made a contribution to the DyCon Blog about "Stochastic optimization for simultaneous control" Take a look the detailed explanation at DyCon…

Master PDE Course – Partial Differential Equations, Control and Numerics

CCM Webinar: Swinging up the double pendulum & Data Driven COVID modeling

Worldwide. 07.05.2020. Last Tuesday on May 05th, 2020, on the CCM - Chair of Computational Mathematics seminars, this time on the online format with a double session webinar about: "Swinging…

Stochastic optimization methods for the simultaneous control of parameter-dependent systems

Umberto Biccari, Ana Navarro-Quiles, Enrique Zuazua. Stochastic optimization methods for the simultaneous control of parameter-dependent systems (2020) Abstract. We address the application of stochastic optimization methods for the simultaneous control of…