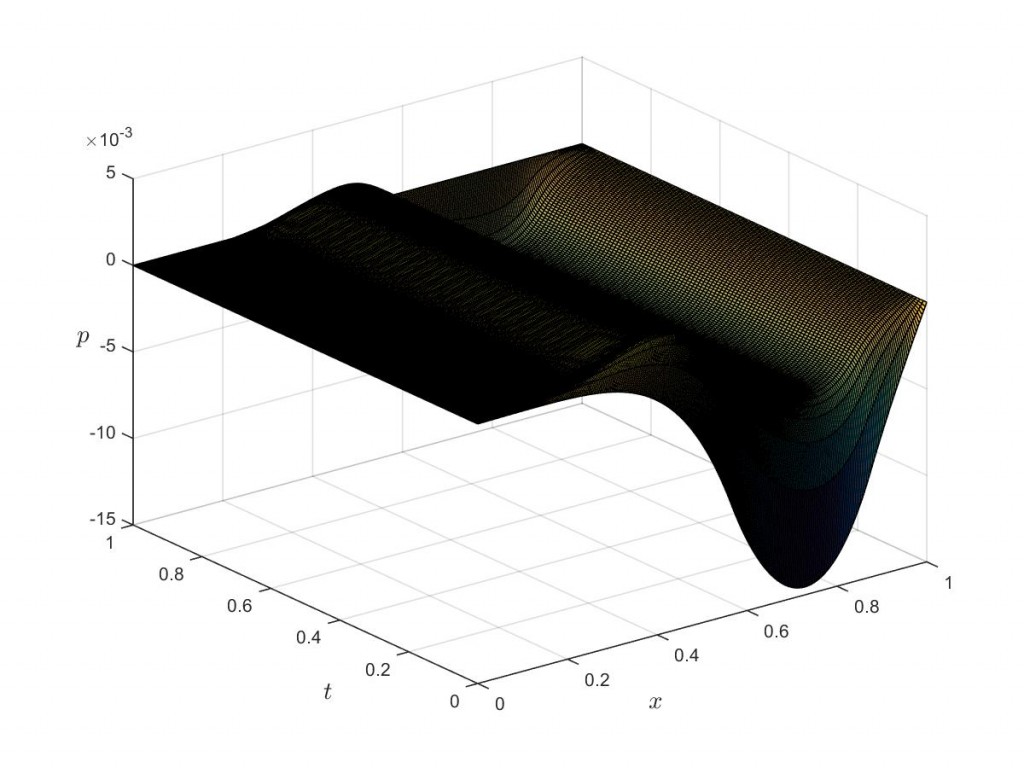
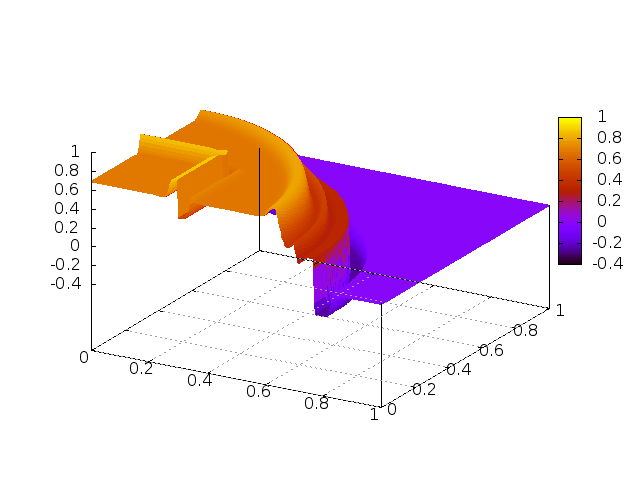
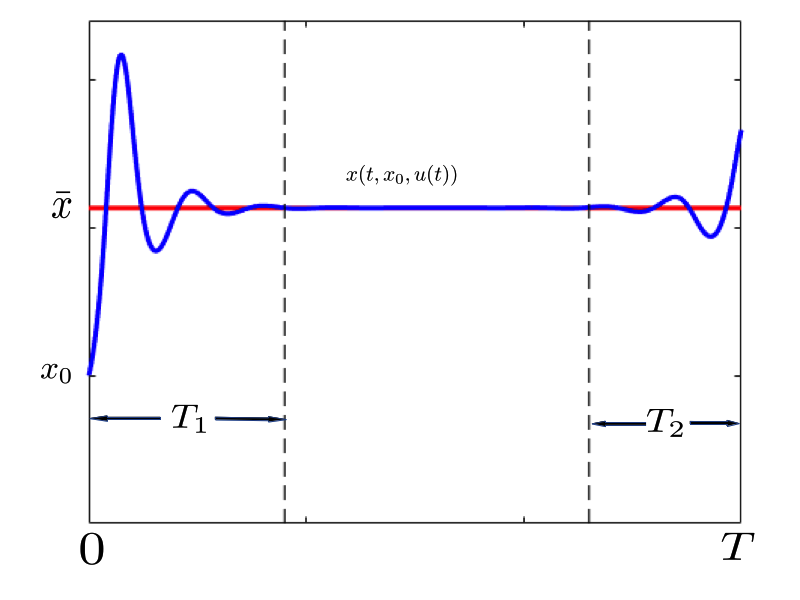
On the decay of one-dimensional locally and partially dissipated and hyperbolic systems
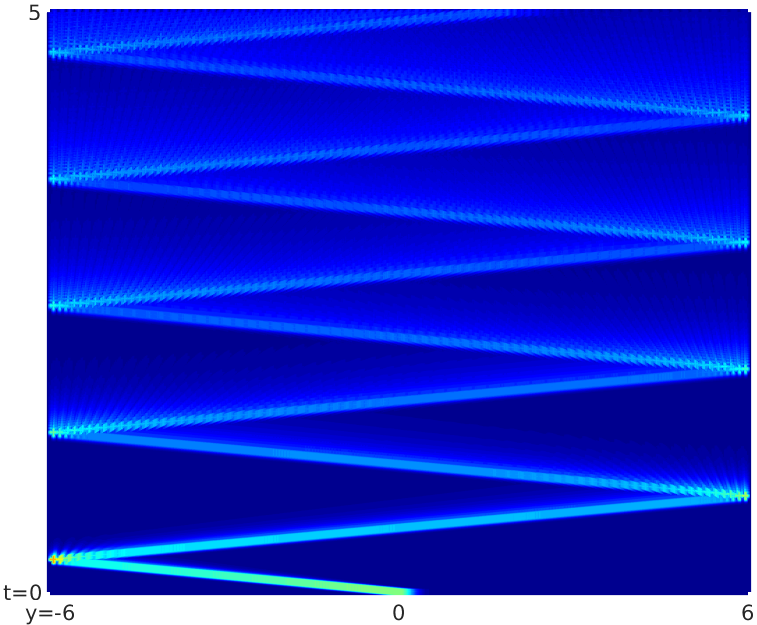
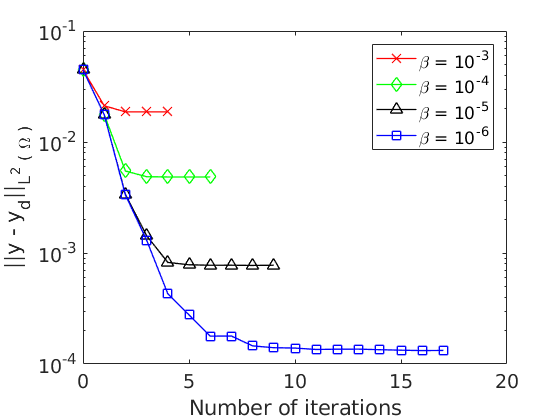
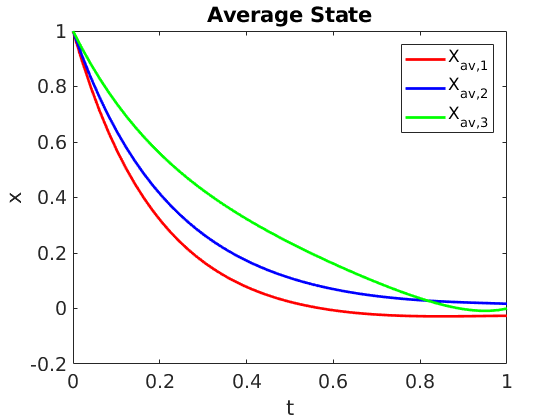
T. Crin-Barat, N. De Nitti, E. Zuazua (2025) On the decay of one-dimensional locally and partially dissipated and hyperbolic systems, ESAIM:COCV, https://arxiv.org/abs/2206.00555 Abstract. We study the time-asymptotic behavior of linear…